TRANSCRIBE: Authenticated Algorithms for Byzantine Agreement
[日本語]
 Abstract
Abstract
Reaching agreement in a distributed system in the presence of faulty processors in a central issue for reliable computer systems. Using an authentication protocol, one can limit the undetected behavior of faulty processors to a simple failure to relay messages to all intended targets. In this paper we show that, in spite of such an ability to limit faulty behavior and no matter what message types or protocols are allowed, reaching (Byzantine) agreement requires at least \(t+1\) phases or rounds of information exchange, where \(t\) is an upper bound on the number of faulty processors. We present algorithms for reaching agreement based on authentication that require a total number of messages sent by correctly operating processors that is polynomial in both \(t\) and the number of processors, \(n\). The best algorithm uses only \(t+1\) phases and \(O(nt)\) messages.
Key words. authentication, reliable distributed systems, Byzantine agreement, consistency, unanimity
Table of Contents
- Abstract
- 1. Introduction
- 2. Histories
- 3. The lower bound result
- 4. Polynomial algorithms using authentication
- 5 Conclusion
- Acknowledgements
- References
- Transcription Note
 1. Introduction
1. Introduction
In this paper we consider algorithms for achieving agreement among multiple processors. The context for this agreement is a network of unreliable processors that have a means for conducting several synchronized phases of information exchange, after which they must all agree on some set of information. We will assume for simplicity that this set of information consists of a single value from some set of values \(V\).
The type of agreement we will study is called Byzantine agreement (LSP), unanimity (Db) or interactive consistency (PSL). It results when in the presence of undetected faulty processors, all correct (nonfaulty) processors are able to agree either on a value or on the conclusion that the originator of the value is faulty. More explicitly, Byzantine agreement is achieved when
- all correct processors agree on the same value, and
- if the sender is correct, then all correct processors agree on its value.
Implicit in I and II is the idea that the agreement is synchronous in the sence that all processors reach this agreement at the same time. In other words, there must be some real time at which each of processors has completed the execution of its algorithm for reaching agreement, and this time must be known and agreed on by all processors in advance.
Our analysis of problem is based on the worst case assumption that faulty processors are not predictable and possibly event malicious. An algorithm should sustain any strange behavior and faulty processors, even collusion to prevent the correct processors fom reaching agreement. Even if the correct processors cannot identify the faulty processors, they must still reach Byzantine agreement. The algorithm should not depend in any way on anticipated behavior of faulty processors.
We establish an exact lower bound for the number of phases of information exchange required. This lower bound \((t+1)\) was known for the case in which only unauthenticated messages are exchanged (FL). We have generalized the proof given by Lynch and Fischer to apply to any kind of message. The lower bound result is somewhat surprising in our context. It indicates that even though we allow correct processors to exchange any kind of verifiable information, an even though we restrict the possible behavior of faulty processors to simply failing to relay messages, Byzantine agreement cannot be reached in \(t\) or fewer phases. Note that if we relax I slightly as in crusader agreement (Da), then we can obtain agreement within two phases.
The algorithms considered provide a method for a single processor to send a single value to all other processors. Generalizations to many processors sending values to each other will be obvious.
We assume some reliable means of communication by which any correct processor can send a message to any other correct processor. For example, this reliability ight be achieved by sending duplicate messages along many paths in a network. In any case, for this paper, unless otherwise stated, we assume a completely connected, totally reliable communication network, and in counting the total number of messages sent, we ignore any duplication or repetition inherent in the communication medium. Note that we only count the messages sent by correct processors.
For algorithms using authentication, we assume a protocol that will prevent any processor from introducing a new value or message into the information exchange and claiming to have received it from another (DH), (RSA). In a typical authentication protocol (PSL), the transmitter appends a signature to the message to be sent. This signature contains a sample portion of the message encoded in such a way that any receiver can verify that the message is authentic and hat it was sent by the sender, but no processor can forge the signature of another. Thus no processor can exchange the content of a message undetectably.
All previous algorithms for reaching Byzantine agreement are exponential in the number of messages (\(O(n^t)\) where \(n\) is the number of processors and \(t\) is an upper bound on the number of undetected faulty processors). The new results presented here include algorithms polynomial in the number of bits exchanged, using authentication. If \(d\) is the number of phases and \(m\) is the total number of messages, then the algorithms previously presented used \(d = t + 1\) and \(m = O(n^t)\).
Lynch and Fischer established a lower bound of \(t+1\) for \(d\), but their proof depends on disallowing any authentication protocol. Here we establish the same lower bound in a general context allowing authentication. Note, however, that our proof does not depend on the use of any particular authentication protocol. In fact it contains no reference to authentication or any other particular type of message.
We present an algorithm for Byzantine agreement with \(d = t+1\) and \(m = O(n^2)\), and a modification with \(d = t + 2\) and \(m = O(nt)\). These algorithms are first presented in the context of a complete network and then generalized to arbitrary networks with sufficient connectivity. The total number of messages is on the order of the number of edges in the network, but more general networks require more phases. Finally we present an algorithm that achieves the lower bound \(t + 1\) for number of phases and also requires only \(O(nt)\) messages.
 2. Histories
2. Histories
In order to give proofs of correctness and especially to establish lower bounds, we will describe the message related behavior of the collection of processors during the phases of information exchange as a single object of directed graphs called phases. We intend the notion of history to capture any synchronous information exchange behavior, including any number of authentication protocols and the exchange of arbitrary message types. The lower bound result of §3 can be extended to asynchronous algorithms with a suitable generalization of the notion of phase.
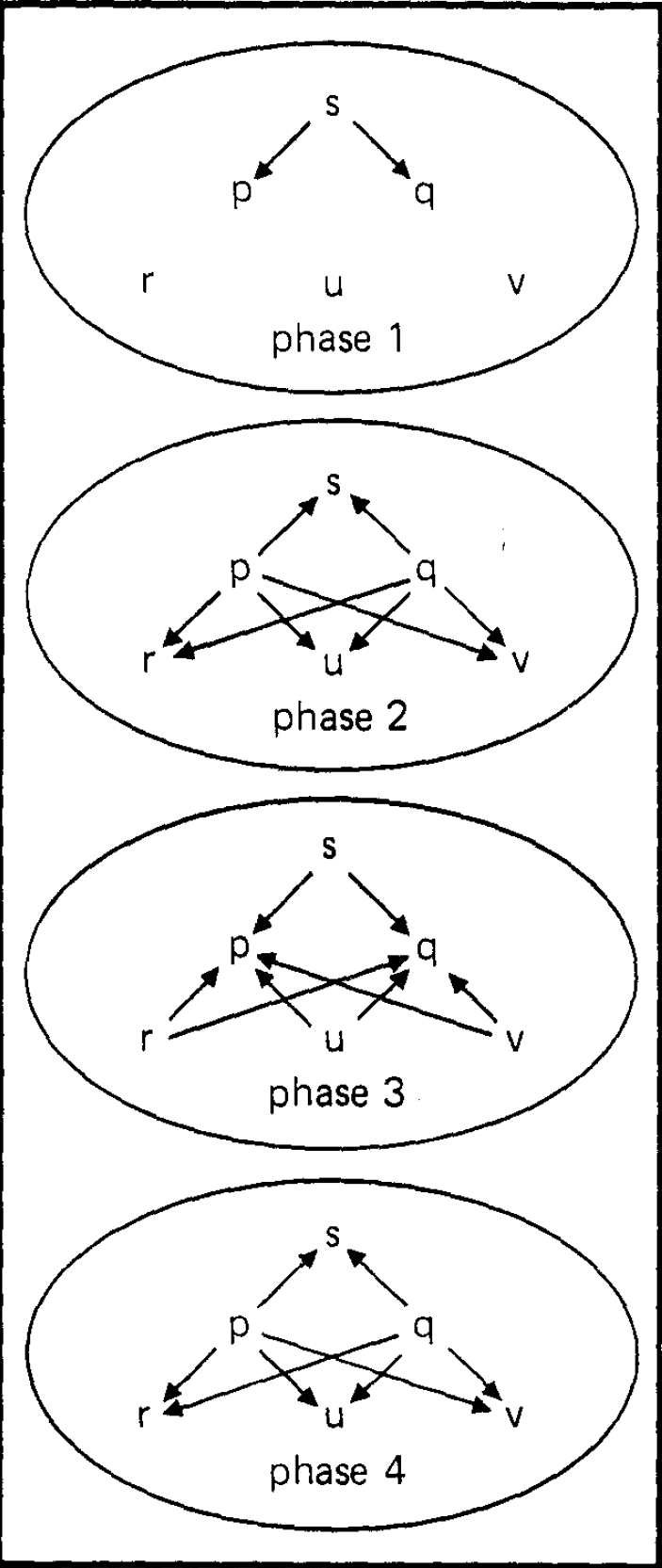
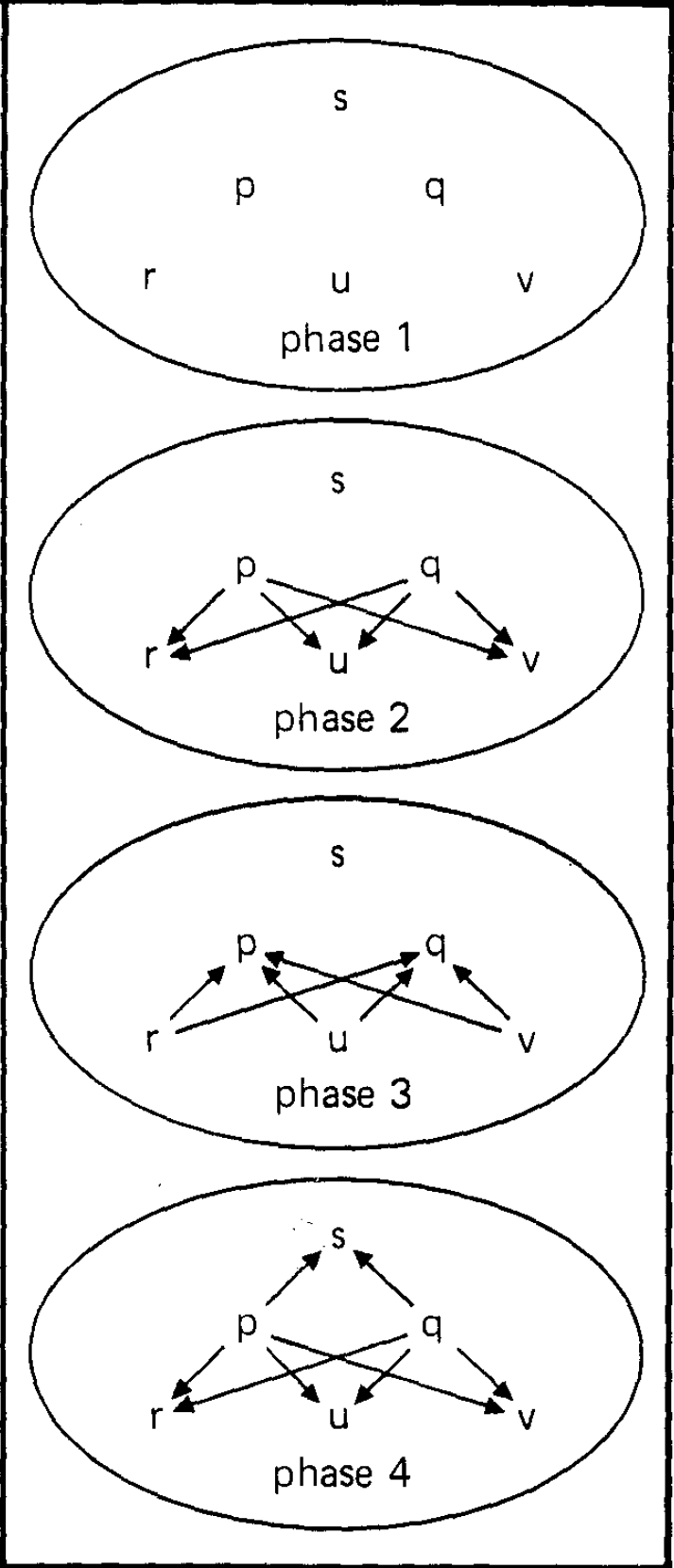
A phase is a directed graph with nodes corresponding to processors and with labels on the edges. A label represents the information sent from a given processor to another during the given phase. We assume that when no messages is sent there is no edge. An \(n\) processor history is a finite sequence of \(n\) node phases, with nodes labelled by the names of the processors, together with a special initial phase called phase 0, such that phase 0 contains only a single inedge to one processor called the sender. (The assumption is that the inedge at phase 0 carries the value that the sender is to send.) Fig. 1 and Fig. 2 represent histories with labels and phase 0 omitted.
A subhistory of a history \(H\) is a copy of \(H\) with some edges removed. From each history \(H\) and processor \(p\) there is a unique subhistory \(pH\) called the subhistory according to \(p\), consisting of only the edges with target \(p\). Thus, the subhistory according to the sender includes the value it is supposed to send even if it sends nothing.
An agreement algorithm on a class of histories \(C\) consist of a correctness rule (a function which given a subhistory according to \(p\) and an edge in a phase to be added to the history as the next phase, produces a possibly empty label for that edge) and a decision function (a function from subhistories according to processors of histories in \(C\) to the union of \(V\) with a symbol 0 representing "sender fault"). With respect to a given correctness rule, a processor \(p\) is said to be correct at phase \(k\) if each edge from \(p\) in phase \(k\) has the label produced by correctness rule operating on the subhistory according to \(p\) of previous \(k - 1\) phases. A processor \(p\) is correct for history \(H\) if it is correct at each phase of \(H\). Observe that the difference between Fig. 1 and Fig. 2 is that in the first, all processors are correct (assuming some appropriate correctness rule) while in the second, the sender is faulty. We call a history \(t\)-faulty (with respect to a correctness rule) if at most \(t\) of its processors are incorrect.
A correctness rule is actually a union of possibly distinct correctness rules, one for each processor. Likewise, the decision function is a union of individual decision functions.
An example of a simple correctness rule is the rule that each processor simply sign and relay (according to the authentication protocol) each incoming message of the previous phase to every other processor.
We say Byzantine agreement can be achieved for \(n\) processors with at most \(t\) faults within \(d\) phases if there is an agreement algorithm for the class \(C\) of \(n\) processor, \(t\)-faulty (with respect to the correctness rule of the algorithm), \(d\) phase histories so that the decision function \(F\) obeys the rules for Byzantine agreement:
- if \(p\) and \(q\) are correct for \(H\) in \(C\) then \(FpH = FqH\), and
- if the sender is correct at the first phase of \(H\) and \(p\) is correct for \(H\) in \(C\) then \(FpH = v\) where \(v\) is the sender's value.
Note that we do not define Byzantine agreement for \(n \lt 3\) or for \(t \gt n\). In the context of an authentication protocol, the class \(C\) of histories is assumed to be limited to those consistent with the semantics of authentication.
 3. The lower bound result
3. The lower bound result
Theorem 1 (LSP). Byzantine agreement with authentication can be achieved for \(n\) processors with an most \(t\) faults within \(t+1\) phases, assuming \(n\gt t+1\).
Proof. For the correctness rule, at phase \(i\) let each node sign and relay every incoming message with \(i\) different signatures to exactly those processors that have not already signed it. Note that messages are distinct even though they carry the same value, if they have travelled distinct paths. The function \(F\), operating on a subhistory, will delete messages that do not confirm to the correctness rule (including those with repeated signatures) and then extract every authenticated (from the sender) value from \(V\) carried by the remaining messages. If exactly one value \(v\) is extracted, then \(F\) will produce \(v\) as output; otherwise, \(F\) will produce 0.
Let \(H\) be a \(t\)-faulty history with \(t+1\) phases, consistent with the semantics of authentication. At the end of phase \(t\), each message carries \(t\) signatures (not counting that of the current recipient). Thus each value that appears in the correct messages of \(H\) will have been seen by some correct processor. Therefore, each correct processor will have the same set of extracted values after \(t+1\) phases. ∎
The following lower bound result is principal result of this section. It shows that the result of Theorem 1 is tight.
Theorem 2. Byzantine agreement cannot be achieved for \(n\) processors with at most \(t\) faults within \(t\) or fewer phases, provided \(n\gt t+1\).
The proof of Theorem 2 is inspired by, but a nontrivial generalization of, the proof given by Lynch and Fischer for the restricted case without authentication (FL). Lynch and Fischer used the \(n \gt 3t\) results of (PSL) to show that any algorithm for Byzantine agreement must be uniform. Assuming uniformity, they established an equivalence relation on their version of \(t\)-faulty histories and obtained a contradiction by showing that too many histories were contained in a single equivalence class. Their proof of this equivalence relied on the ability to preserve equivalence while changing one message at a time. Their proof of this ability, without using the uniformity assumption, is essentially the proof of the base case in the induction that follows.
Proof of Theorem 2. Assume that Byzantine agreement can be achieved for some \(n\gt t+1\) within \(t\) phases. Let \(R\) be the correctness rule and let \(F\) be the decision function on subhisories such that \(\langle R,F\rangle\) achieves Byzantine agreement on \(n\) processor, depth \(t\), \(t\)-faulty histories.
Let \(C\) be the class of \(n\) processor, depth \(t\), \(t\)-faulty histories that have a critical sequence such that all incorrect processors appear on the sequence and any incorrect node appears at or after level corresponding to the order its label appears on the sequence. The class \(C\) contains histories that exhibit serial faultiness, in the sense that tha set of faulty processors is allowed to increase by at most one processor per phase, starting with no faults before phase 1, and once allowed in the set these faulty processors may exhibit their faultiness at any node corresponding to a phase at or after their entry. Note that any nodes corresponding to such a faulty processor may be correct.
Define an equivalence relation on histories in \(C\) by saying \(H\) is equivalent to \(H'\) if, whenever \(p\) is correct for \(H\) and \(q\) is correct for \(H'\), then \(FpH'=FpH\). Note that \(C\) includes histories in which all processors behave correctly. Since we assume \(V\) has more than one value, this means that there must be histories in \(C\) that are not equivalent. But, as we will show, \(C\) is a single equivalence class. Under an appropriate definition of \(\langle R,F\rangle\), both Fig. 1 and Fig. 2 could describe histories from the set \(C\). However, in Fig. 2 the result of the algorithm must be independent of any information from the sender since the sender sends nothing. This fact is the key idea behind the contradiction we obtain.
We say that a processor is hidden at phase \(k\) if it has not outedges at \(k\) or any later phase. We will also refer to the node at phase \(k\) as hidden if the processor is. In particular we will show by induction on the phase \(k\) that, if \(r\) is a node representing a processor at phase \(k\) of history \(H\) in \(C\), then:
- there is a history \(H'\) in \(C\), equivalent to \(H\), identical to \(H\) through phase \(k\) except for outedges of \(r\), with \(r\) correct and all processors correct after phase \(k\); and
- if all other nodes at phase \(k\) are correct, then there is a history \(H'\) in \(C\), equivalent to \(H\), identical to \(H\) through phase \(k\) except for outedges of \(r\), with \(r\) hidden and all other processors correct after phase \(k\).
Note that if a processor labels a hidden node, then changing the information on its inedge cannot affect the subhistory according to any other processor. In Fig. 2 the sender is hidden at phase 1.
In short we will show by induction that we can corect a node at any phase or hide a node if all other nodes at its phase are correct, and that the resulting history will be in \(C\) and equivalent to the one from which we started, while all changes will be to the outedges of the particular node and to edges at later phases. Thus we will have shown that every history in \(C\) is equivalent to any history in which the root is hidden and all other processors are correct.
Case 1. Let \(k=t\).
Let \(r\) be an incorrect node at phase \(k\) of history \(H\) in \(C\). If we correct the outedges of \(r\) one at a time, then for each individual change there is a processor correct for \(H\) that sees the same subhistory after the change as before. Thus each individual change preserves equivalence with \(H\). Since we cannot make any correct node incorrect, each individual change preserves membership in \(C\). Changes are only made to the outedges of \(r\). The final result \(H'\) has \(r\) correct and all processors trivially correct after \(k\).
Let \(r\) be a node at phase \(k\) in history \(H\) and \(C\) and let all other nodes at phase \(k\) be correct. Proceeding as in (a), we remove the outedges of \(r\), one at a time. Here we may change \(r\) from correct to incorrect but since there were no other incorrect nodes at phase \(k\) we could replace the \(k\)th entry in the critical sequence by the label of \(r\), preserving membership in \(C\). The rest of the argument is the same as that for (a).
Case 2. Assume the induction hypotheses (a) and (b) for all phases after \(k\).
Let \(r\) be an incorrect node at phase \(k\) of a history \(H\) in \(C\). The following steps will reserve membership in \(C\) and equivalence to \(H\) and change only outedges of \(r\) and edges at later phases.
- Correct all nodes after phase \(k\) (induction hypothesis (a)).
- While incorrect outedges of \(r\) remain,
- replace position \(k+1\) in the critical sequence by \(s\), a target of an incorrect outedge \(e\) from \(r\);
- hide \(s\) at phase \(k+1\) (induction hypothesis (b));
- correct \(e\) (some correct processor will see the same subhistories both before and after the change);
- correct all nodes at phase \(k+1\) (induction hypothesis (a)).
The final result \(H'\) will have \(r\) and all processors after phase \(k\) correct.
Assume all processos correct at phase \(k\) and let \(r\) be a node at phase \(k\). The following steps will preserve membership in \(C\) and equivalence to \(H\) and change only outedges of \(r\) and edges at later phases.
- Correct all nodes at phase \(k+1\) (induction hypothesis (a)).
- Replace the \(k\)th position in the critical sequence by the label of \(r\).
- While outedges of \(r\) remain,
- replace position \(k+1\) in the critical sequence by \(s\), a target of an outedge \(e\) from \(r\);
- hide \(s\) at phase \(k+1\) (induction hypothesis (b));
- remove \(e\) (some correct processor will see the same subhistories both before and after the change);
- correct all processors after phase \(k\) (induction hypothesis (a)).
- Hide the processor labelling \(r\) at phase \(k+1\) (induction hypothesis (b)). The final result \(H'\) will have \(r\) hidden at phase \(k\) and all other processors after phase \(k\) correct.
This completes the proof of Theorem 2. ∎
Remark. Whenever it is defined, Byzantine agreement can be achieved for \(n\) processors within \(n-1\) phases. Thus the provision \(n \gt t+1\) is necessary for the lower bound of Theorem 2.
 4. Polynomial algorithms using authentication
4. Polynomial algorithms using authentication
As mentioned in the introduction, we assume the existence of some authentication technique that prevents faulty processors from undetectably changing the content of messages.
For purposes of counting messages we supply the following specific syntax for the labels on the edges of directed graphs called phases.
- The set of values \(V\) is contained in the set of atomic messages.
- A label is either an atomic message (an authentication) or a sequence of labels.
- An authentication is a label of the form\[ ({\rm label} \ a) p,\] where \(p\) is the name of a processor and \({\rm label}\ a\) is a label.
- A sequence of labels is a label of the form\[{\rm label}\ a, {\rm label}\ b,\] where \({\rm label}\ a\) and \({\rm label}\ b\) are labels.
Note that \((a,b,c)p\) is not the same label as \((a)p\), \(b(p)\), \((c)p\).
A label \(a\) is part of label \(b\) if either:
- \(a=b\);
- there is a label \(c\) and a processor or \(p\) such that \(a\) is part of \(c\) and \(b=(c)p\);
- there are labels \(c\) and \(d\) such that \(b=c\), \(d\) and \(a\) is part of \(c\) or \(d\).
A message is a label with no commas.
Thus, at any phase any processor can send any message to any other processor, except that no processor can alter an authenticated message received at a previous phase and forward it as an authenticated message received at a previous phase and forward it as an authenticated message at the next phase, nor can any processor pretend to have received an authenticated message it did not receive and forward that as an authenticated message. In the rest of this paper, attention will be restricted to histories consistent with the semantics of authentication. In particular, if \((a)q\) is part of a label on an edge from processor \(p\) then either \(p=q\) or \((a)q\) appears as part of a label on an inedge to \(p\) in a previous phase.
The basic idea behind the following two algorithms is to minimize the number of messages on each edge by restricting the cases in which a processor must relay a message. In the proof of Theorem 1, we assume a complete graph, so that when a correctly authenticated value is revealed to a correct processor, all correct processors will have it at the next phase. For Theorem 3 we restrict the number of values about which a processor must relay information. For Theorem 4 and 5 we restrict the paths over which messages travel so that when a correct processor receives a correctly authenticated value, other correct processors will receive it within some constant number of phases. Finally, for Theorem 6, we restrict the number of processors that are required to relay information. In this case when a correct relay processor receives a correctly authenticated value, the others will receive it one phase later, but correct processors that are not relay processors may receive the value long before it is known to the others.
Let \(e\) be the number of edges in the directed graph that has an edge between two processors exactly when our algorithm may require some message along that edge.
Theorem 3. Byzantine agreement can be achieved for \(n\) processors with at most \(t\) faults within \(t+1\) phases using at most \(O(e)=O(n^2)\) messages.
Proof. Our correctness rule will be a restriction of that of the proof of Theorem 1 so that no processor relays more than two messages to any other, regardless of the number of messages received or the number of distinct paths incoming messages may have travelled. At the beginning of phase \(i+1\), each processor totally (lexicographically) orders all messages during the previous phase, discarding messages that are not of the form \((\cdots ((v)p_1)p_2 \cdots)p_i\) where \(v\) is a value not seen before, \(p_1\) is the signature of the sender, and all signatures are distinct. If a message carrying value \(v\) is not discarded, then the processor is said to extract \(v\). If the processor has not yet relayed any messages, then it relays the first two with distinct values (the first one if there are not two distinct values). If the processor has relayed only one message during all previous phases, then it relays the first of its messages. The relay process consists of signing the message and forwarding it to all those whose signatures do not already appear in the message. A processor relays a value only if it is either the first or the second diferent value extracted. Once a processor has relayed two distinct values, it stops processing messages for the algorithm and at the end it will decide "sender fault," i.e. the decision function \(F\) from the proof of Theorem 1 will produce 0 for this processor. If it gets through \(t+1\) phases without extracting any value, \(F\) will also produce 0; but if it has extracted exactly one value \(v\), then \(F\) will produce \(v\).
Each correct processor sends at most two messages over each edge. Thus, the total number of messages sent by correct processors is bounded by twice the number of edges, \(e\).
If the sender correctly sends \((v)s\) to each other processor, then authentication prevents faulty processors from importing more valeus, so \(F\) will produce \(v\) for each correct processor. If at phase \(t+1\) a correct processor receives and does not discard a message of the form \((\cdots ((v)p_1)p_2 \cdots)p_{t+1}\), then the first \(t\) processors on the list of signatures must be faulty, so the last one must be correct and all other correct processors have simultaneously received the same message. If, at the end of \(t+1\) phase, a correct processor has extracted only one value, then each correct processor has extracted only that value, and the decision function \(F\) will produce the same value for each correct processor. If any correct processor extracts more than one value, then all will. Consequently, although the sets of extracted values may not agree, they yield sufficient information to reach Byzantine agreement. ∎
If we restrict the number of possible edges to \(e=O(nt)\) by restricting the edges available for transmission we can reduce the number of messages. First we show a simple way to achieve this reduction that requires one extra phase.
Theorem 4. Byzantine agreement can be achieved for \(n\) processors with at most \(t\) faults within \(t+2\) phases using at most \(O(nt)\) messages.
Proof. We further restrict the correctness rule of the proof of Theorem 3 by arbitrarily choosing \(t+1\) processors to be relay processors and requiring any nonrelay processor to send messages only to relay processors (the sender is not a relay processor). Now the number of messages is \(O(nt)\). If a correct processor extracts a new value by phase \(t+2\), then some correct processor extracted that value by phase \(t\), some some correct relay processor extracted it by phase \(t+1\). Thus by phase \(t+2\) every correct processor must have extracted only that value. As in the proof of Theorem 3, although the sets of extracted values may not agree, they yield sufficient information to reach Byzantine agreement. ∎
The restricted network used in the proof of Theorem 4 is a \(t+1\) connected graph. It is straightforward to show that the graph must be at least \(t+1\) connected in order to reach Byzantine agreement (Da), (Db). In (LPS) \(t+1\) connectivity was shown to be sufficient using an exponential number of messages. Here using methods similar to those of (LPS) we generalize the algorithm of the proof of Theorem 4 to show that \(t+1\) connectivity is sufficient even for a polynomial number of messages.
The diameter of a graph is the least upper bound of the lengths of shortest paths between pairs of vertices, where by length we mean the number of edges. If a graph is \(k\) connected, then there are at least \(k\) vertex disjoint paths between any pair of vertices. The \(k\)-diameter of a graph is the least upper bound of the lengths of the \(k\) shortest vertex disjoint paths between pairs of vertices.
Theorem 5. If \(d\) is the \((t+1)\)-diameter of a \((t+1)\)-connected network of \(n\) processors with at most \(t\) faults, then Byzantine agreement can be achieved within \(t+d\) phases using at most \(O(e)\) messages.
Proof. We use the correctness rule and the decision function of Theorem 3, restricted of course so that only available edges of the graph are used for messages. If a processor extracts a new value at phase \(t+i\), then some correct processor has extracted a value by phase \(t\), so each correct processor will have extracted it (or two others) by phase \(t+d\). Again, each edge carries at most two messages, so the total number of messages is \(O(e)\). ∎
Now we return to our assumption of a complete network and present our best algorithm for Byzantine agreement with authentication.
Theorem 6. Byzantine agreement can be achieved on a complete network in \(t+1\) phases with \(O(nt)\) messages.
Proof. If \(n \gt 2t+1\) then \(O(n^2)=O(nt)\) so we are done by Theorem 3. Assume \(n \gt 2t\). We choose \(2t+1\) processors including the sender to play active relos and let all the others be passive. The correctness rule for the active processors is that of Theorem 3, except that they must ignore all messages signed by passive processors. The passive processors are not to send messages. The decision function for active processors is that of Theorem 3. Thus they reach Byzantine agreement among themselves by phase \(t+1\).
Passive processors modify the decision function so that it also counts the number of active processors that have sent more than one message, producing 0 if this number is at least \(t+1\). Passive processors discard the same messages as active processors, but they extract only values that have been signed (in the total collection of messages received) by at least \(t+1\) distinct active processors. Note that if a passive processor receives a message at phase \(t+1\) and does not discard it, then it will extract the value carried by that message because the \(t+1\) signature must occur in that message. However, if a message is received at an earlier phase and not discarded, its value may not be extracted until later confirming messages supply \(t+1\) distinct signatures.
If the correct active processors never extract a value, then the correct passive processors will never extract one because there are at most \(t\) faulty active processors. If any correct active processor extracts a new value then some correct active processor extracts that value by phase \(t\) and relays it to all. If a processor extracts a value at phase \(t\), then the message it relays will contain the signature of \(t+1\) active processors; otherwise, if it extracts the value by phase \(t-1\), then at least \(t\) other correct active processors will have extracts the value by phase \(t\). Thus if any correct active processor extracts onl one value, then each correct active processor extracts only that value and each correct passive processor will be able to extract that and only that value by phase \(t+1\).
If every correct active processor has extracted more than one value by phase \(t\), then the passive processors will have received more than one message from \(t+1\) active processors by phase \(t+1\).
The only difficult case is that in which each active processor extracts more than one value by phase \(t+1\), but some correct active processor has not extracted more than one value by the end of phase \(t\). It remains to show that in this case, the passive processors will be able to extract more than one value.
In this case, no correct active processor can extract more than one value by phase \(t-1\). At least two values are extracted by phase \(t\) (possibly by different processors). If the two values are extracted at phase \(t\), then the passive processors will extract them at phase \(t+1\). But at least one of them is extracted at phase \(t\). Moreover, if some correct active processor has extracted \(v\) by phase \(t-1\), then each correct active processor has extracted \(v\) or nothing by phase \(t-1\). Thus, if the first value is extracted at phase \(t\) or if all correct active processors extract that first value by \(t-1\), then the passive processors will be able to extract two values.
This leaves the case this \(v\) is extracted by some but not all correct active processors by phase \(t-1\). Each of the correct active processors that extracted \(v\) relays it to the passive processors by phase \(t\). If one of the processors that did not extract \(v\) by phase \(t-1\) extracts two other values at phase \(t\), the passive processors can extract those two values. Otherwise, each of the processors that did not extract \(v\) by phase \(t-1\) will extract \(v\) at phase \(t\) and relay it to the passive processors. In any case the passive processors will extract at least two values. ∎
 5 Conclusion
5 Conclusion
The lower bound of \(t+1\) phases with authentication means that we must look elsewhere to achieve Byzantine agreement quickly. In fact we must relax some requirement because the lower bound of Theorem 2 applies no matter what kind of message we send. Although the proof is given in the context of synchronous phases, any purported asynchronous algorithm for Byzantine agreement would certainly be imbeddable within the synchronous phase context by simply imposing the phases on its behavior.
One possibility would be to look at algorithms that probably achieve Byzantine agreement. In a probabilistic context, if we had a realistic upper bound \(t\) on the number of possible faults, then we would likely also have information on the probability of exactly \(t\) faults, exactly \(t-1\) faults, etc.
While they do not reduce the minimum number of phases required, our algorithms do reduce the total number of messages required for Byzantine agreement from exponential to polynomial in the number of processors or in the number of bits exchange by correct processors. It would be useful o find algorithms that stop after a smaller number of phases whenever possible.
We have not established a tight lower bound on the number of messages required in the worst case. In (DR) lower bounds on the number of messages and the number of signatures that must be exchanged in order to obtain Byzantine agreement are obtained. The algorithm in (DR) requires fewer messages than ours but uses more phases.
 Acknowledgements
Acknowledgements
The authors thank Nancy Lynch for helpful suggestions about this manuscript. The proof of Theorem 6 uses suggestion of Lynch made in private correspondence with respect to a different problem. Subsequent to the completion of the proof of Theorem 2 in its present form, the authors received a private communication from Michael Merritt containing a somewhat similar proof of this result.
 References
References
- (DH) W. Diffie and M.Mellman, New direction in cryptography, IEEE Trans. Inform. Theory, IT-22 (1972), pp.644-654.
- (Da) D.Dolev, The Byzantine generals strike again, J. Algorithms, 3 (1982), pp.14-30.
- (Db) ─, Unanimity in an Unknown and unreliable environment, Proc. IEEE 22nd Symposium on Foundations of Computer Science, 1981, PP.159-168.
- (DR) D. Dolev and R. Reischuk, Bounds on information exchange for Byzantine agreement, Prof., ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing, Ottawa, Aug. 1982. See also IMB Research Report RJ3587 (1982).
- (FL) M. Fischer and N. Lynch, A lower bound for the time to assure interactive consistency, Inform. Proc. Letters, 14 (1982), pp. 183-186.
- (L) L. Lamport, using time instead of timeout for fault-tolerant distributed systems, Tech. Rep., Computer Science Laboratory, SRI International, June 1981.
- (LSP) L. Lamport, R. Shostak and M. Pease, The Byzantine generals problem, ACM Trans. Programming Languages and Systems, to appear.
- (PSL) M. Pease, R. Shostak and L. Lamport, Reaching agreement in the presence of faults, J. Assoc. Comput. Mach., 27 (1980), pp.228-234.
- (RSA) R. L. Rivest, A.Shamir and L. Adleman, A method for obtaining digital signatures and public-key cryptosystems, Comm. ACM, 21 (1978), pp.120-126.
Transcription Note
A 1983 paper on asynchronous Byzantine atomic broadcast. A transcription of an old PDF for the purpose of reading it in machine translation.
- DOLEV, D. STRONG H. R. Authenticated algorithms for Byzantine agreement. SIAM Journal on Computing, 1983, 12.4: 656-666.