論文翻訳: Merkle Search Trees: Efficient State-Based CRDTs in Open Networks
École Normale Suprieure
Paris, France
alex.auvolat@inria.fr
Univ. Rennes, Inria, CNRS, IRISA
Rennes, France
francois.taiani@irisa.fr
 ABSTRACT
ABSTRACT
最近の CRDT 技術の多くは、操作デルタの配信を保証するために因果ブロードキャストプリミティブ (caucal broadcast primitive) に依存している。しかしながら、このようなプリミティブは、メンバーシップの追跡が困難な大規模オープンネットワークでは効率的に実装することが困難である。この論文ではその代替策として、状態を特殊なマークル木としてエンコードすることで純粋な状態ベース CRDT を効率的に実装でき、このアプローチは多くのノードが参加/離脱する可能性のあるオープンネットワークに適していることを主張する。我々の貢献の核心は、キーの順序を維持しながら平衡検索木を実装する新しい種類のマークル木であるマークル検索木 (MST; Merkle Search Tree) である。この後者の特性により、多くのアプリケーションで一般に発生する連続したキーの集合に対する更新ケースで特に効率的となる。我々はこの新しいデータ構造を使用して分散イベントストアを実装し、更新頻度の低い非常に大規模なシステムでその効率性を示す。特に、いくつかのシナリオにおいて我々のアプローチはベクタークロックアプローチと比較して帯域幅コストを 66% 削減し、一貫性レベルを 34% 向上させることを示している。最後に、オープンネットワーク上の分散データベースにおける我々の構成の他の用途を提案する。
索引用語 ─ マークル木、検索木、CRDT、IoT、地理分散システム、ピアツーピア、アンチエントロピー
Table of Contents
- ABSTRACT
- I. 導入
- II. 文脈と関連研究
- III. マークル検索木データ構造
- IV. 大規模オープンネットワークにおける CRDT
- V. アプリケーション: 因果一貫性分散イベントストア
- VI. 実験的評価
- VII. 結論と展望
- ACKNOWLEDGEMENTS
- References
- 翻訳抄
 I. 導入
I. 導入
大規模地理分散システム [1][2] の登場により、一貫性とスケーラビリティを両立したデータレプリケーション技術への関心が高まっている。中でも Conflict-free Replicated Data Types (CRDT) [3] は、開発者に自然でモジュール化されたプログラミングパラダイスを提供しながら結果整合性 (eventual consistency) を実現する能力において際立っている。
CRDT は並行操作を事後的に結合できる解決ルールを提供することで、同期処理なしに複製が並行して操作を実行することを可能にする。このため CRDT は結果整合性を備えた弱い一貫性システムを構築するために使用できる。
最近の CRDT 技術は主に因果ブロードキャストプリミティブとベクタークロック (Vector Clock) を活用することで、操作デルタの信頼性のある因果配信を保証することに重点を置いており [4][5]、これにより二つの完全な状態を直接比較する必要がない。しかし、これらのアプローチは多くのノードが参加・離脱するオープンネットワークでは限界がある。これは因果ブロードキャストプリミティブとベクタークロックはどちらもそのような状況には適していないためである。最近になってようやく因果ブロードキャストがスケーラブルな形で動的構造を持つネットワークに拡張された [6] が、このアプローチの実用性はまだ実証されていない。一方、ベクタークロックはネットワークに参加した過去および現在のノードの数に比例して増加するメタデータを必要とし、これは大規模な最適化を行った場合でも重要なスケーラビリティ障壁となる [7]。
これらの制限を回避しながらオープンネットワークを対象とするために、この論文では因果ブロードキャストもベクタークロックも必要としない純粋な状態ベース CRDT に焦点を当て、この根本的な問題である「事前の相互作用がなく互いの状態について何も知らない可能性のあるノード間での大規模なリモート状態マージを実装する方法」に焦点を当てる。この問題は CRDT を形式化する以前に研究されていたアンチエントロピー (anti-entropy) と類似している。以下ではアンチエントロピー、状態マージ、状態調整 (state reconciliation) という用語を同じ意味として使用する。より具体的には、我々は他の CRDT セマンティクスと組み合わせることができる 2 つの基本的な構成要素である集合またはマップを実装する CRDT を対象とし、2 つの非常に大規模な集合またはマップ間の差異を低レイテンシーかつ最小限の帯域幅使用で解決することを目指す。
集合とマップの調整のための一般的な戦略は、集合間の差異を迅速に識別するために使用できるハッシュベースのデータ構造 [9] であるマークル木 [8] を使用する。しかし、マークル木を使用する通常のアンチエントロピーアルゴリズムは要素の順序を保持しないため、近接する項目の連続に更新を適用する場合に特に非効率となる。これは非常に一般的なシナリオであり、基本的な例としては要素がタイムスタンプによって順序付けられたイベントである場合が挙げられる。
この論文では、項目の集合から決定論的に平衡検索木を構築し、それをマークル木として符号化するマークル検索木 (Merkle Search Tree) と呼ぶ新しいデータ構造を用いることでこの根本的な課題を克服することを提案する。我々は、マークル探索木を使用してすべての接続されたノードに過去のすべてのイベントの最終的な配信を保証する因果一貫性のあるイベントストアを構築する方法を実証する。我々はこの手法をベクタークロックベースの手法 [10]、および順序を保持しないマークル木構成と比較し、大規模ネットワークにおいて低から中程度の更新率の下でマークル検索木が最良のトレードオフを提供することを示す。我々のシミュレーションでは、ベクタークロック手法と比較して帯域幅使用量が 66% 削減され、一貫性測定では 34% の改善、99 パーセンタイル配信遅延では 32% の改善が示された。順序を保持しないマークル木と比較した場合、マークル検索木は 3 つの指標すべてにおいてより優れていることが示された。
 II. 文脈と関連研究
II. 文脈と関連研究
我々の研究は、このセクションで紹介する分散システム、データベース、ファイルシステムなどのよく研究されているドメインに基づいている。
 A. CRDT と CAP 定理
A. CRDT と CAP 定理
CRDT [3] は結果整合性アルゴリズムを定式化できる汎用的なフレームワークである。CAP 定理 [11] [12] は、分散システムが強い一貫性、可用性、ネットワーク分断耐性の 3 つの特性のうち 2 つしか達成できないことを述べている。CRDT ベースのシステムは通常、複製が一時的に分岐することを許容することで、強い一貫性より可用性を重視する。システムが使用する特定の CRDT は、信頼性のある通信が可能になり次第、分岐状態にある複製が自動的に一意の共有状態に調整する方法を定義する。
この論文では CRDT を複製状態における結合半順序集合 (join-semilattice) として定式化する。すなわち、CRDT は対象結合演算子 \(\sqcup\) を持つ可能な状態の集合 \(\mathbb{V}\) である。状態 \(x \in \mathbb{V}\) に対する操作は \(\sqcup\) にしたがって \(x\) を厳密に上位の状態 \(x'\) に変更することあり、つまり \(x'=x \sqcup o\) となるような項目 \(o \in \mathbb{V}\) が存在する状態である。たとえば、実装したいデータ型が成長専用集合 (grow-only set) である場合、\(\mathbb{V}\) は可能な集合の空間であり、\(\sqcup\) は和集合演算子である。集合 \(x\) に要素 \(e\) を追加することは \(x\) を状態 \(x' = x \cup \{e\}\) に変更することである。
演算子 \(\sqcup\) はまた、異なるノードで実行された並行操作を結合し、それらを決定論的に解決するためにも使用される。あるノードが状態 \(x_1\) にあり、別のノードが状態 \(x_2\) にある場合、両方のノードの状態は \(x_1 \sqcup x_2\) (これは \(x_2 \sqcup x_1\) と同じ) に解決される。例えば成長専用集合 CRDT の場合、マージ操作は集合の和集合として定義され、結果の状態はすべてのノードで追加されたすべての項目を含む集合として定義される。より複雑な CRDT を定義することで削除や異なるデータ型 (マップやカウンターなど) などの追加操作を実装できる。必要な要件は可換、結合、冪等な結合演算子 \(\sqcup\) を実装することだけである。
この研究では集合 CRDT とマップ CRDT に焦点を当て、異なる 2 つのノードに \(x_1\) と \(x_2\) がある場合の \(x_1 \sqcup x_2\) の効率的な計算を実装する方法を考察する。ここで効率はネットワークラウンドトリップ数と帯域幅の使用量によって測定される。
 B. ゴシップアルゴリズム
B. ゴシップアルゴリズム
アンチエントロピープロトコルは一般的に伝染型調整戦略 (epidemic reconciliation strategy) を採用している。これは、分散システムのノードが合意された状態に収束するためにランダムに選択された他のノードと繰り返し差異を調整する戦略である [13]。我々はこの戦略を採用して CRDT を実装し、ゴシップアルゴリズムを CRDT 状態マージ演算子と組み合わせてすべてのノードでの最新の最終配信を保証する。ゴシップアルゴリズム [13] は大規模分散システムにおけるデータ配信の効率的なスキームであり、ランダムピアサンプリング [14] と組み合わせて使用するとオープンネットワークに適している。ゴシップアルゴリズムはよく研究された配信特性を持ち [15] 分散コンピューティングの基盤として広く利用されている [16]。
 C. ハッシュ関数とマークル木
C. ハッシュ関数とマークル木
ハッシュ関数とそれが生成するチェックサムはデータの識別や完全性・真正性の検証に広く用いられている。そのため、異なるコンピュータ上に存在するデータを比較し、効率的な分散調整メカニズムの実装に役立つ自然な選択のように思われる。しかし非常に大きなデータ片を検証するには、データ全体に対してハッシュ関数を計算する必要があり、これは典型的な Key-Value データストアのような大規模な分散オブジェクトを扱う場合には特にコストのかかる提案である。このコストを削減するため、データをチャンクに分割し、各チャンクを個別にハッシュする方法があるが、その場合、単一のハッシュだったものがデータサイズに比例して増加するハッシュのリストに置き換えられることになるため、依然として問題は残る。
この線形コストを克服するため Merkle [8] はデータをチャンクに分割し、ハッシュツリーを計算することで大規模なデータをハッシュ化する手法を方法を導入した。ハッシュツリーにおいて、葉はデータチャンクのハッシュ、中間ノードはそれぞれの子ノードの値の連結のハッシュとなる。単一のルートハッシュですべてのデータを識別することができ、1 つのブロックの妥当性は対応する葉への経路をたどることで確認できる。木が適切に平衡していれば、対数個のハッシュのみを検証すれば良い。この検証はデータ全体にアクセスすることなく実行することも可能である。
元のマークル木は二分木だが、マークル木の核となる原理は一般化され他の文脈にも適用できる。特に ZFS [17] や IPFS [18] などのプロジェクトはファイルシステム全体の真正性と完全性を保証するためにマークル木のような再帰ハッシュを利用している。このようなデータ構造の再帰ハッシュによりデータの重複排除も可能にする [17][18]。この場合、マークル木はノードが複数の親を持つ DAG となる。
分散システムにおいてマークル木は特に有用であることが示されている。データセットをマークル木に符号化する決定論的な方法が与えられれば、2 つのノードはルートハッシュを交換して比較するだけで同じバージョンのデータを持っているかどうかを判断できる。バージョンが異なる場合、同じ内容を表す枝は両方のノードで同じハッシュを持つため、データセットの異なる部分のみを交換できる。
マークル木には様々な形状がある。標準的な二分マークル木は番号付きのデータブロックの列を識別・交換するために使用できるが、2 つのノードに存在するキーセットが異なる場合、任意のキー空間で効率的に差異を検出することができない。Dynamo [9] などのデータベースシステムは任意の Key-Value のマッピングからなる状態を交換・修復するためにマークル木を使用するが、木が適切に平衡することを保証するためにキーの順序を破壊し、キーをハッシュ化して一様分布に投影する必要がある。これにより、近接するキーのシーケンスが更新されるシナリオではこの方法は最適ではない。任意のキー範囲で平衡を保ちながらキー順序を保持するマークル木構造は [19] で導入されたが、この方法は決定論的ではない。同じデータセットで複数のマークル木表現が存在する可能性があり、これはアンチエントロピーには適さない。任意のキー範囲でキー順序を保持する最初の決定論的平衡マークル木の構築は二分ツリープ (binary treap) [20] を使用して導入された。我々が提案する構成は、より広いツリーノードで同じ性質を実現し、より浅い木を作成してリモート差分計算に必要なラウンドトリップ数を削減する。これにより、二分マークル木と比較して計算・保存する必要のあるハッシュ数も削減される。
 D. B-Tree
D. B-Tree
我々が提案するマークル検索木は、いくつか重要な違いはあるものの、B-Tree [21] に類似した構造を用いる。B-Tree は関連データベース管理システム (RDBMS) で使用される索引データ構造である。B-Tree は大きな出次数を持つノードによって浅い検索木を実装し、標準的な二分検索木よりも高速な探索を可能にする。ノードは通常、ツリーノードの機械表現がメモリページのサイズとなるような出次数を持つ。B-Tree において、ノードはキー空間の分割方法を定義する値の集合と、分割の各区間の値を含む部分木へのポインタの集合で構成される。我々が導入するマークル検索木にも子ノードのキー空間を分割する役割を果たす値を含む中間ノードを含んでいる。しかし、これらの中間ノードの大きさは一定ではなく、その大きさは確率的な境界を持つだけである。
 E. その他の最新手法とその限界
E. その他の最新手法とその限界
マークル木に基づかないリモートデータ集合比較のための他の手法も提案されている。特に、集合差分を計算するための数学的手法は十分に研究されているが、ブルームフィルタ [22][23] を用いた近似的な差異検出に限定されていたり、データセット全体に対して高コストな計算を必要とするなど制約が厳しいものであったりする [24]。実際には、典型的なアンチエントロピープロトコルは 2 つのノード間の更新の欠落を識別を検出 [10] するためにベクタークロック [25] を用いているが、DottedDB [7] で使用されるような大規模な最適化を施したとしても、ベクタークロックは過去および現在の参加者の総数に比例するメタデータを必要とせずにデータセットの 2 つのバージョン間の分岐を特定することができない。
 III. マークル検索木データ構造
III. マークル検索木データ構造
大規模なマップや集合を実装する CRDT の効率的な調整手順を実装するため、我々はマークル検索木 (MST と表記) と呼ぶ木構造を提案する。これは、我々の知る限り以下の 3 つの特徴を組み合わせた初めての木構造である:
与えられた項目の集合は、木として一意の決定論的表現を持つ。
キーの順序が保持される。
木は常に (確率的に) 平衡している。
これらの特性の組み合わせにより、アンチエントロピーのための木のリモート比較が極めて効率的となる。
 A. MST 構成
A. MST 構成
マークル検索木は全順序空間 \(\mathbb{K}\) から抽出した要素による順序集合を実装する。マップを実装するために、要素は集合 \(\mathbb{V}\) (値; この場合、\(\mathbb{K}\) はキーの集合) のタグを付与することができる。\(\mathbb{V}\) には、マップに \(f:\mathbb{K}\to\mathbb{V}\) にキーが存在しないことを示すためのデフォルト要素 \(\bot\) を含む。
MST 構成は任意のバイト列に対するハッシュ関数に基づいている。このハッシュ関数は衝突耐性を前提としており、同じハッシュを持つ 2 つの列が見つかる確率は無視できると仮定する。これはマークル木の構成に不可欠な一般的な仮定である。我々はまた、ハッシュ関数のサイズが \(B\) のべき乗である特定の区間の値に一様に射影されると仮定する。この追加の性質は、ハッシュ関数を空間 \(\mathbb{K}\) 上の決定論的乱数源を提供するという二次的な目的にも使用するため、我々の構成に必要である。これらの特性は両方とも SHA-512 などの最新のハッシュ関数によって実際に実現されている。
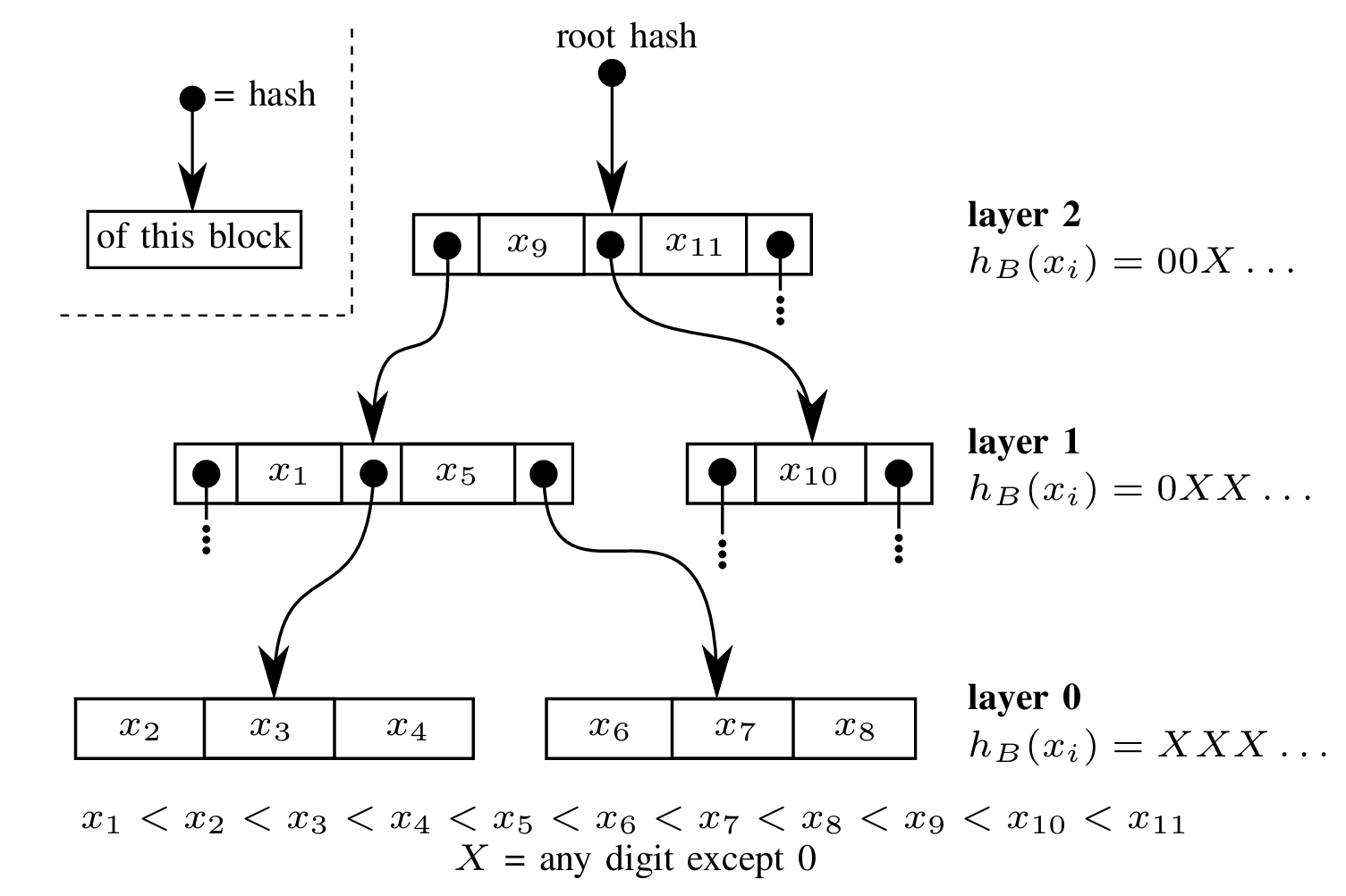
MST は検索木であり、内部のツリーノードが複数の値を持ち、その値が \(\mathbb{K}\) のパーティションを定義し、そのパーティション内で子の値が分離されるという点で B-Tree に似ている。木は層に分割され、層 0 は葉ノードの層に対応する (Figure 1)。層 1 のツリーノードは連続する項目のブロックであり、その境界は \(l' \gt l\) の項目に対応する。例えば Figure 1 では、層 0 の最初のノードには境界 \(x_1\) と \(x_5\) の間に含まれる値 \(\{x_2\), \(x_3\), \(x_4\}\) が格納されており、\(x_1\) と \(x_5\) はレイヤー 1 に格納されている。以前の構成 [20] と同様に、値をハッシュすることで得られる決定論的なランダム性を使用して木の形状が決定される。MST に格納される値は、ハッシュを計算し、その値を基数 \(B\) の進数で記述することによって層が割り当てらる。これを \(h_B(x)\) と呼ぶ。項目 \(x\) が割り当てられる層 \(l(x)\) は、\(h_B(x)\) においてゼロのみで構成される最長プレフィクスの長さと同じ番号の層である。
 B. MST の単一性と演算
B. MST の単一性と演算
ここまで我々が記述した構成は決定論的である。つまり、与えられた項目の集合に対して MST としての可能な表現は一つしか存在しないしないことを意味している。これは調整手順を実装するために重要な性質である。標準的な演算の実装はこの定義から導かれる。
MST をマップとして使用する場合、木 \(f\) 内の単一の項目に対する読み取り操作 \({\tt get}(f,k)\)、連続する項目の範囲に対する読み取り操作 \({\tt getrange}(f,[k_0,k_1))\)、書き込み操作 \({\tt put}(f,k,v)\)、\({\tt delete}(f,k)\) を効率的に実装できる。put 操作によって項目 \(x\) が非葉層 \(l \gt 0\) に挿入される場合、下位層 \(l' \lt l\) のツリーノードの一部は境界 \(x\) で 2 つに分割する必要があるかもしれない。同様に、非葉層で値が削除される場合、階層の一部のノードを結合する必要があるかもしれない。与えられた put 操作または delete 操作に対して、各層 \(l' \lt l\) で最大 1 回の分割または結合しか発生しないため、これらの操作の複雑さは木の深さに比例する。
構造的単一性 (structural unicity) の結果として、同じ要素を異なる順序で挿入しても常に同じ表現に収束し、ルートのマークルハッシュも同じになる。構造的単一性は中間ノードでも有効である。2 つの中間ノードが同じマークルハッシュを持つのは、これらのノードから始まる部分木にまったく同じ項目が含まれている場合のみである。したがって、2 つの木を比較して差異を探す際に同じマークルハッシュを持つ部分木が見つかった場合、それらの間に差異がないことが分かるため、それらの部分木全体をスキップできる。
 C. 構造的特性: 平衡と深さ
C. 構造的特性: 平衡と深さ
基数 \(B\) で数値を書き出す、定数長の列に一様に投射するハッシュ関数を使用するため、項目が層 \(l\) にある確率は \(p_l=\left(\frac{1}{B}\right)^l \frac{B-1}{B}\) となる。層 \(l\) における値の平均数は、層 \(l+1\) に置ける値の平均数の \(B\) 倍であることは容易に分かる。層 \(l\) の値は層 \(l' \gt l\) の値を持つ境界で分割されるため、層 \(l\) のノードには平均して \(B-1\) 個の値が格納され、非葉層では \(B\) 個の子ノードが存在する。ノードがこれらの平均値よりもはるかに多くの値と子ノードを持つ確率は指数的に減少するため、ノードサイズを任意の高い確率で制限できる。
木の深さは項目を割り当てることのできる最大レベルである。層 1 に項目が存在する確率は \(np_l\) に制限され (ここで \(n\) は木の要素数)、これは \(l\) の増加とともに指数的に減少する。したがって木の深さは \(\log_B n\) に定数 \(c\) を加えた値に制限でき、その確率は \(c\) の増加と共に指数的に減少する。
木の深さは約 \(\log_B n\) であり、ノードは高い確率で一定数の項目を持つため、木は適切に平衡した構造を持ち、読み取り、書き込み、削除は \(O(\log_B n)\) の計算量で実装できると結論づけられる。
 D. データセット比較の効率性
D. データセット比較の効率性
2 つの異なるノードに格納された 2 つのマークル検索木の比較は効率的である。ノード \(n_1\) 上の \(f\) と \(n_2\) 上の \(g\) を比較する場合、ノード \(n_1\) と \(n_2\) は \(O(d \log_B n)\) 個のメッセージのみを交換する必要がある。ここで \(d\)=\(|\{x\ \mid\) \(f(x)\) \(\ne\) \(g(x)\}|\)、\(n=\max(|f|,|g|)\) である。\(\mathbb{K}\) と \(\mathbb{V}\) の要素が一定サイズであると仮定すると、交換されるメッセージの平均サイズは \(B\) に比例する。
内部のツリーノードの平均出次数は \(B\) の値を変更することで制御できる。\(B\) の値を大きくすると、より多くのノードを含むノードととなり、ピア間で交換する際により多くの帯域幅を必要とするが、木は浅くなるため葉にいたるノードの完全なセットを取得するためのネットワークラウンドトリップ数が少なくなる。我々の実験では \(B=16\) に固定している。
 E. CRDT としてのマークル検索木
E. CRDT としてのマークル検索木
\(\mathbb{V}\) が \(\forall x\), \(\bot \sqcup_{\mathbb{V}} x = x \sqcup_\mathbb{V} \bot = x\) となるような結合操作 \(\sqcup_\mathbb{V}\) を持つ CRDT である場合、マークル検索木は \(\sqcup_\mathbb{V}\): \((f \sqcup g)(x)\) = \(f(x) \sqcup_\mathbb{V} g(x)\) の点対点適用によって定義される \(\mathbb{K}\to\mathbb{V}\) 上の CRDT を実装する。
CRDT が取る状態の列は、セクション II-A で説明したように、\(\sqcup\) に対して単調であることが想定される。状態 \(x\) から状態 \(x'\) への遷移は \(x' = x \sqcup o\) の形式でなければならない。マークル検索木の場合、これは許可される操作の集合を、各個のキーに対して単調なシーケンスにつながる操作のみに制限することを意味する。したがって、put および delete 操作を直接使用してはならず、代わりに更新は \({\tt update}(f,k,v)\) = \({\tt put}(f,k,{\tt get}(f,k)\sqcup v)\) の形式を使用する必要がある。
\(\mathbb{V}\) を適切に選択することで様々な CRDT を得ることができる。例えば \(\mathbb{V}=\{\bot,\top\}\) を項目が存在するかどうかを示すブール値とすると \(\mathbb{K}\) 上で定義される成長専用集合を得る。\(\mathbb{V}\) がバージョン番号を持つ last-write-wins レジスタである場合、last-write-wins 調整を持つ Key-Value ストアが得られる。既存の CRDT 型はいずれも値型 \(\mathbb{V}\) として使用でき、異なる項目を効率的に検出するマップ CRDT 構成を実現する。
 IV. 大規模オープンネットワークにおける CRDT
IV. 大規模オープンネットワークにおける CRDT
我々が提示したマークル検索木は、集合 CRDT またはマップ CRDT に対して、特に効率的なペアワイズ分散調整手続き (pair-wise distributed reconciliation procedure) を実装するために使用できる。この手順により、2 つのノードは自発的な交換に基づいて、他のノードの状態を事前に知る必要なく一意の状態に収束することができる。この手順を単純なゴシップベースのアルゴリズムと組み合わせることで、高いチャーン率 (high churn rate) を持つオープンネットワークにおける効率的な更新配信を可能にする。
 A. 状態ベース CRDT のゴシップベース調整
A. 状態ベース CRDT のゴシップベース調整
我々の手法は MST を使わない ALGORITHM 1 の基本形式に示される状態ベース CRDT の単純な分散状態更新手法に基づいている。ALGORITHM 1 はリアクティブゴシップ戦略を採用している。ノードが \(x_0\) から \(x_1\) へ状態遷移を伴う操作を行う場合 (ここで \(x_1 = x_0 \sqcup o\) とする)、これは \(x_1\) をいくつかのランダムピアにゴシップする。ノードが状態 \(x'_0\) にあるときに状態 \(x_1\) を受信すると、\(x'_0 \sqcup x_1 = x'_1\) への遷移を行い、\(x'_1 \ne x'_0\) の場合、今度は \(x'_1\) をいくつかのランダムピアにゴシップする。ランダムピアの選択には、ネットワークからランダムに選ばれたノードの ID を取得できるピアサンプリングサービス [14] を前提としている。
ALGORITHM 1 はリアクティブ push 専用交換を実装する。pull または push/pull 戦略を用いる他の方法も可能であり、チャネルを周期的なコンポーネントで拡張して従来のアンチエントロピープロトコルを実現することもできる。

 B. マークル検索木を使用した大規模 CRDT の実装
B. マークル検索木を使用した大規模 CRDT の実装
ALGORITHM 1 を使用して集合や Key-Value ストアなどの大規模マップ型 CRDT を実装する場合、状態全体を交換するような単純な実装はすぐに扱いにくくなる。このような場合、MST を用いることで、ノード間の複数回のラウンドトリップをコストにするだけで、ネットワーク帯域幅の使用量を大幅に削減できる。ALGORITHM 2 は、ローカル操作をブロックすることなくバックグラウンドでこれを実現する方法を示している。マージに必要なリモート情報がすべて取得されるまで (12 行目) この状態に対して get 操作や update 操作を実行し続けることができる。このアルゴリズムでは、マージしたいリモート MST のセットがバッファに保持され (4, 14, 18 行目)、欠落しているすべてのブロックがリモートピアに要求される (13 行目)。すべてのブロックがローカルで利用可能になると、ネットワーク通信成しにマージ操作が実行され (16 行目) ローカル MST が更新される。

 C. 因果一貫性
C. 因果一貫性
ALGORITHM 1 と ALGORITHM 2 は次の意味で因果一貫性を実装する: ノードが状態 \(x\) から読み取りを行った後、\(x\) から \(x' = x \sqcup o\) への遷移を生じる操作を行った場合、put 操作の因果過去 (causal past) は \(x\) に含まれていると記述でき、put を観測する他のすべてのノードは自身の因果過去 \(x\) (\(x'\) は \(x\) を含むため) または \(\sqcup\) に従って \(x\) の後継を観測する。このアルゴリズムの結果として得られる特性は、マージ \(\sqcup\) によって定義されるすべての CRDT に適用可能であり、マークル検索木はこれを CRDT のマップに自然に拡張する。これは因果ブロードキャスト [6][26] で要求されるように、ネットワークトポロジーにいかなる条件も付けずに行われる。これはすべてのゴシップイベントで完全な状態マージが行われるという事実から生じる。
因果一貫性が不要で結果整合性で十分な場合、ALGORITHM 2 は個別の操作をゴシップし、受信と同時にそれらを適用し、一方で完全なデータ構造の定期的なマージを並列実行することで最適化できる。この場合、定期的なマージは結果整合性を保証するための最終メカニズムとして機能する。明示的なマージを使用することで、帯域幅を節約するためにゴシップのファンアウトや単一操作の生存時間 (TTL) を、ネットワークカバレッジが 99% になる値まで削減し、ゴシップイベントを見逃す少数のノードに対するアンチエントロピー手順として完全マージ操作を利用することができる。
 D. クラッシュに対する注意
D. クラッシュに対する注意
ALGORITHM 2 は帯域幅を確保するために同時実行可能なマージ操作の数に制限を設けている (8 行目)。そのため、クラッシュしたノードからの応答を待っている場合にアルゴリズムがスタックする可能性がある。同時マージの制限を取り除くことは実際には望ましくない。これは、帯域幅の使用が多数の並行ペアワイズマージに薄く分散され、高いテイルレイテンシを引き起こす可能性があるためである。したがって、ノードがクラッシュした場合にマージをキャンセルするには、障害検出器 (fault detector) または近似障害検出器 (approximate fault detector) を使用する必要がある。ノードがクラッシュしておらず単に遅いだけの場合は Safety に違反しないため、操作をキャンセルしても問題ない。ただし、終了 (結果整合性) を達成するにはノードが少なくともいくつかのマージ操作を完了できる必要がある。
 E. 分散 MST への拡張
E. 分散 MST への拡張
マークル検索木は関数型プログラミングの意味で永続データ構造 (persistent data structure) である。これは、\({\tt put}(k,v)\) を実行する際に、取得した MST は以前の MST を置き換える必要がなく、共通ブロックのメモリ共有により両方の MST を低いストレージコストで同時に利用可能に保てることを意味する。この場合のハッシュは従来のポインタと類似の役割を果たすが、重要な違いは、ハッシュ値が同じ値を含む部分木の重複を自動的に委譲するために使用でき、ハッシュ値が計算されたマシンノード以外でも意味を持ち続けることである。この論文では MST を単一マシンノードに格納されるローカルデータ構造として使用しているが、上記の特徴を利用して分散 MST (Distributed MST) を実装することもできる。
1) 格納場所: 分散 MST (または D-MST) は、例えば DHT を使用してデータ構造がネットワークの多くのマシンノードに分割された MST である。これは IPFS [18] で導入された任意のマークル DAG データ構造であれば容易に実現でき、二分検索木ではすでに既に実現されている [19]。我々の場合、ツリーノードは DHT に独立して格納され、それらのハッシュによって識別されるブロックに対応する。キャッシュを使用しない場合、D-MST はすべての操作で \(O(\log_B n \times \log m)\) 回のネットワークラウンドトリップを必要とし (\(m\) はネットワーク内のノード数)、キャッシュを利用することで、好条件下 (チャーンなし) の get 操作では \(O(\log_B n)\) まで削減できる [19]。
2) ガーベッジコレクション: D-MST シナリオでのガーベッジコレクションはローカル MST の場合よりも困難である。選択肢の一つは、保存されているすべてのブロックを一定時間後に期限切れとし、データ構造を操作して有効期限カウンタをリセットする分散キープアライブ機構を備えることである。このようなシステムの詳細は本論文の範囲外である。
 V. アプリケーション: 因果一貫性分散イベントストア
V. アプリケーション: 因果一貫性分散イベントストア
ALGORITHM 2 で構築された CRDT の利点を、因果一貫性分散イベントストア (Causally-consistent Distributed Event Store) (因果ブロードキャストの概念をカプセル化するデータ構造) を例に挙げて説明する。因果ブロードキャストは分散アルゴリズムの基本的なプリミティブであり、通常は送信/受信ネットワークプリミティブとベクタークロック [5] を用いて直接実装される。これらは我々の手法に対する主要な代替手段であり、効率的にスケールしないことが示されている。完全性を期すため、因果ブロードキャストの代替手法として静的オーバーレイ [26] が存在することを指摘する。静的オーバーレイは最近、動的な設定に拡張された [6] が、この最新の開発の実用性はまだ実証されていない。
因果ブロードキャストは \(\delta\)-CRDT [4] などの操作ベース CRDT の構成要素であることが多い。このセクションではこの従来の視点を逆転させる。因果ブロードキャストの配信特性を保証するためにメッセージパッシングアルゴリズムを配備して分散オブジェクトを実装する代わりに、システムによって生成されるすべてのイベントを格納するイベントストア (event store) と呼ぶストレージを構築することで因果ブロードキャストを提供する。我々は、互いの状態について事前知識を持たない 2 つのピア間で欠落した更新をアドホックに効率的に伝播させる方法としてマークル検索木を活用する。このようなシステムを直接的に応用することで、例えばピアツーピアのチャットルームやログシステムを構築できるが、より高度なアルゴリズムのプリミティブとしても使用できる。
以下では、このような手法の理論的複雑性を研究し、[10] で導入されたベクタークロックを用いるアンチエントロピーアルゴリズムである Scuttlebutt (スカットルバット) と比較する。我々は次のセクションでこの解析を実験的に確認する。どちらの手法も大規模ネットワークにおける更新伝播を保証するために push-pull ゴシップ戦略を採用している。我々の理論的解析は TABLE II にまとめられている。
| \(n\): 過去のイベント数 |
| \(d\): アンチエントロピーラウンドの新イベント数 |
| \(p\): 過去と現在のノード数 |
| \(m\): 現在接続しているノード数 |
| \(\lambda\): ネットワークレイテンシ |
| アンチエントロピーアルゴリズム | 拡散時間 | アンチエントロピーラウンドごとの転送量 |
|---|---|---|
| Scuttlebutt | \(2\lambda\log m\) | \(O(p+d)\) |
| マークル検索木 (我々) | \(2\lambda\log m\log_B n\) | \(O(d\log_B n)\) |
 A. Scuttlebutt アンチエントロピー
A. Scuttlebutt アンチエントロピー
1) アルゴリズム: ログ内のイベントはプロデューサーのマシンノード識別子とプロデューサーによってローカルに生成されたシーケンス番号のペアで識別される。Scuttlebutt はリアクティブ pull-push 設計を採用している。つまり、各プロデューサーノードごとに保持している最後のシーケンス番号のベクトルをマシンノードが交換することで新しいイベントが伝播する。この交換により、マシンノードは他のノードに送信する欠落イベントの正確な集合を計算できる。
2) 拡散時間: アンチエントロピーラウンドは 1 ラウンドトリップの時間で完了する。ゴシッププロトコルはネットワーク全体に到達するのに平均 \(\log m\) ステップを必要とする。ここで \(m\) な現在ネットワークに存在するノード数である。したがって、総拡散時間は \(2\lambda \log m\) であり、\(2\lambda\) はラウンドトリップ時間である。
3) 帯域幅使用量: 最初のステップの帯域幅使用量は \(O(p)\) である。ここで \(p\) はシーケンス番号を送信する必要のあるプロデューサーノードの数を表す。どのノードがまだネットワークに参加しているかを知る方法がないため、つまり \(p\) はこれまでのネットワークに参加したすべてのノードの数に等しくなる。2 番目のステップでは、欠落している \(d\) 個のイベントのみを送信する必要があるため、使用される帯域幅は \(O(d)\) である。したがって、総帯域使用量は \(O(p+d)\) となる。
 B. マークル検索木アンチエントロピー
B. マークル検索木アンチエントロピー
1) アルゴリズム: マークル検索木は単純な成長のみを行う集合として用いられる。\(\mathbb{V}=\{\bot,\top\}\) は現在の項目に対して設定されるブール値、\(\mathbb{K}\) はイベント空間であり、イベント生成時のタイムスタンプ (論理クロックまたは実時間近似値) によって順序付けられる。結果として、最も最近に生成されたイベントは木の一方の端に配置され、アクセスの局所性が向上する。ゴシップアルゴリズムは ALGORITHM 2 で説明したものである。
2) 拡散時間: 変更がなければアンチエントロピーラウンドは 1 ラウンドトリップ時間で完了する。変更が存在すれば、アルゴリズムは新しい項目ごとに木の葉を参照する必要があるかもしれない。木の深さは高い確率で \(\log_B n\) (+小さな定数) であり、ここで \(n\) は木に格納されたイベント数である。アルゴリズムは木の各レベルごとに 1 往復を必要とするため、アンチエントロピーラウンドは \(\log_B n\) ラウンドトリップ時間で完了する。ゴシッププロトコルはネットワーク全体に到達するために平均 \(\log m\) ステップを必要とするため、総拡散時間は \(2\lambda\log m \log_B n\) となる。
3) 帯域幅使用量: 一方のノードから要求され、他方のノードによって送り返されるマークル木のノードの総数は \(d\log_B n\) によって制限されるため、1 回のアンチエントロピーラウンドの総帯域幅使用量は \(O(d\log_B n)\) となる。
 VI. 実験的評価
VI. 実験的評価
このセクションではマークル検索木を使用した大規模分散イベントストアをシミュレーションする実験について説明し、他の既存の手法と比較する。オンラインで利用可能な我々のシミュレータ1は、アクターベースの設計を採用しており、すべてのマークル検索木アルゴリズムを含む約 2000 行の Elixir コードで構成される。
 A. 方法論
A. 方法論
我々は同期通信ラウンドでクラッシュのない 1000 ノードのネットワークをシミュレートした。イベントは、ネットワーク内でランダムに選択されたノード上で、タイムスタンプが増加する形で生成される。2 つのシナリオを考察した。最初のシナリオではネットワーク全体で 1 ラウンドあたり平均 0.1 イベントのレートでイベントが生成され、二つ目のシナリオでは 1 ラウンドあたり平均 1 イベントのレートで生成される。
我々は、我々のアルゴリズム (セクション V-B) を 2 つの競合アルゴリズムと比較した。一つ目はセクション V-A で説明した Scuttlebutt 調整アルゴリズム、二つ目はマークル木の 2 番目の構成である、項目のハッシュに基づくマークル符号化されたプレフィクス木 (マークルプレフィクス木 (Merkle Prefix Tree) または MPT) である。
MPT アルゴリズムはマークル検索木と同じ方法で欠落要素を検出し、同じゴシックベースのアルゴリズムを使用する。マークル検索木との主な違いは、MPT がキー値をハッシュしてからプレフィクス木を構築することで構成されるため、この構成法ではキーの順序が保持されないことである。しかし、ハッシュプレフィクスの衝突確率はプレフィクス長とともに指数関数的に減少するため、平均的に平衡の取れた木を構築する。
実験は TABLE III に示すように、異なるアルゴリズムパラメータで複数回実行される。
我々の目的は、変更された値が類似のキーを持つ場合、マークル検索木の順序特性が中間ノードの送信数を少なくするため、アンチエントロピーアルゴリズム性能が向上することを示すことである。分散イベントの場合、新しいイベントはタイムスタンプが最も高いイベントとなり、ツリーの右側にコンパクトな部分木を形成する。一方、ハッシュのプレフィクス木を使用した場合、イベントはランダムに分散され、新しく追加された葉への経路は少数の中間ノードのみを共有する。
| 共通パラメータ | |
|---|---|
| ノード数 | 1000 |
| ラウンドあたりに生成されるイベント数a | 0.1 (TABLE IV, Figure. 2, Figure 4) 1 (TABLE V, Figure 3) |
| Scuttlebutt アンチエントロピー | |
| ファンアウト | 1†, 2*, 4 |
| ゴシップ間隔 | 1*, 2, 4†, 8 ラウンド |
| MST と MPT のアンチエントロピー | |
| ファンアウト | 6 |
| 最大同時マージ | 1, 2, 3, 4*†, 6, 8 |
- 1https://gitlab.inria.fr/aauvolat/mst_exp/
- aネットワーク全体で
 B. イベント拡散の測定指標
B. イベント拡散の測定指標
ネットワークにおけるメッセージ拡散の不整合を評価するために、二値エントロピーの定義に基づく指標を定義する。特定のシミュレーション時間ステップにおけるネットワークのエントロピーは、各メッセージに対して、そのメッセージを受信したノードの割合の二値エントロピーの合計として定義される。より形式的には、\(M\) をメッセージの集合とし、\(p_m\) をネットワーク内のノードのうちメッセージ \(m \in M\) を受信した割合とすると、我々が用いるエントロピー測定は次のように定義される: \[ \begin{eqnarray} H & = & \sum_{m \in M} H_b(p_m) \nonumber \\ & = & \sum_{m\in M} -p_m \log_2 p_m - (1-p_m)\log_2(1-p_m) \end{eqnarray} \]
この指標では、エントロピー値が低いほどイベントの拡散が均一であり、したがってネットワーク全体の状態の一貫性が高いことを示す。
 C. 結果
C. 結果
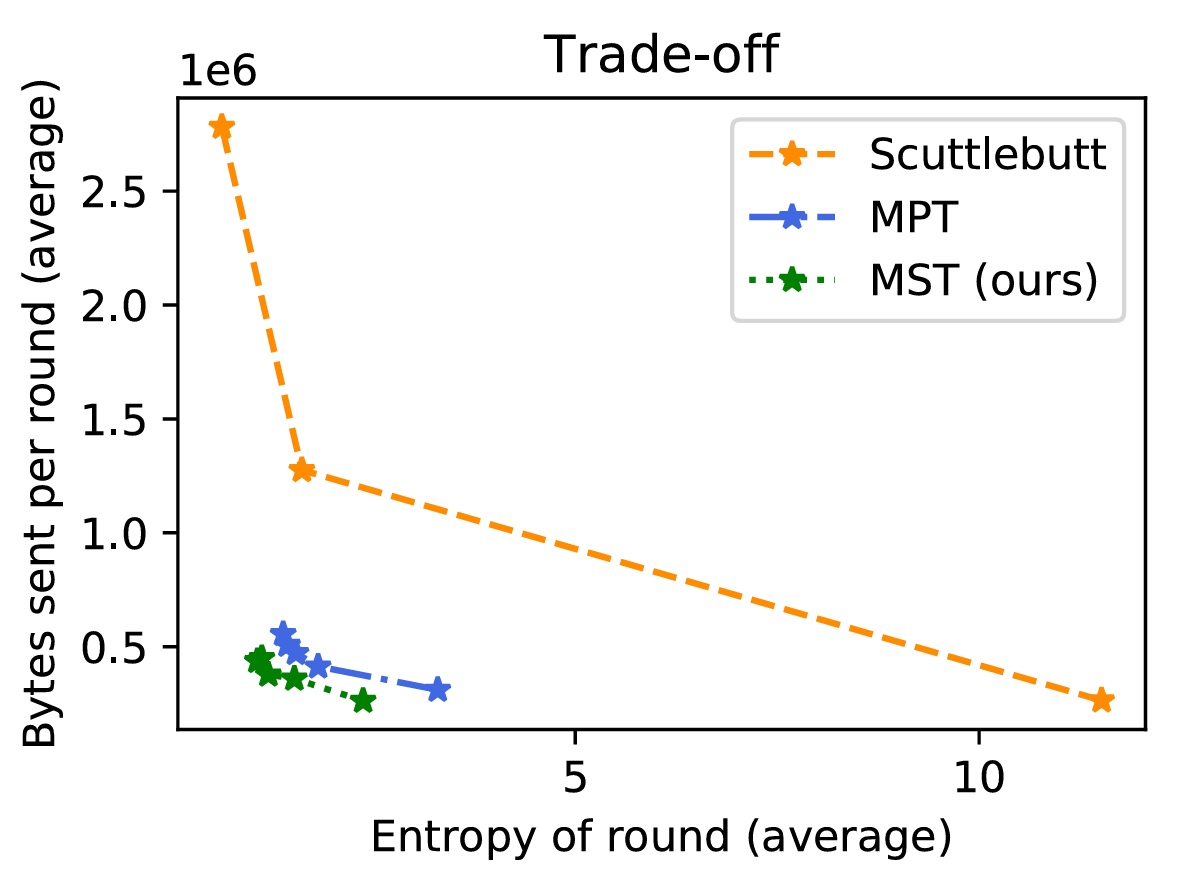
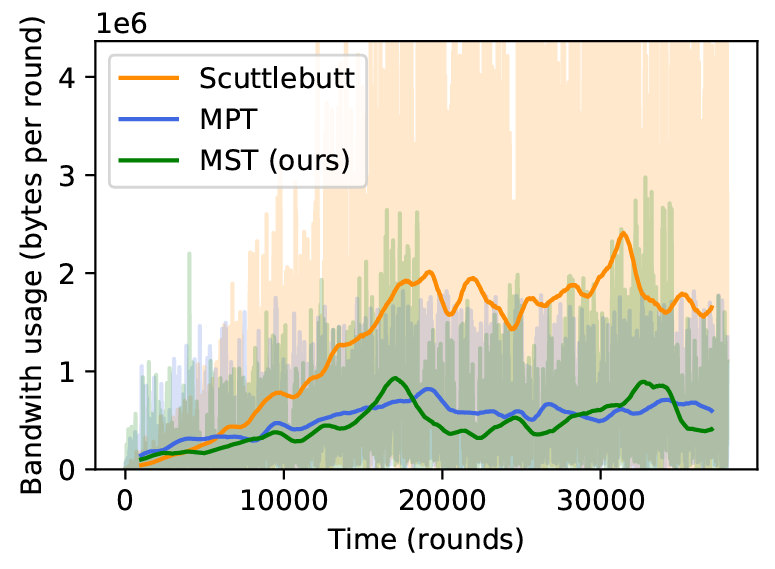
1) エントロピーと帯域幅のトレードオフ: イベント発生率が低い最初のシナリオは、マークル検索木アプローチにとって最も好適なシナリオである。Figure. 2 はこのシナリオにおいてアルゴリズムの様々パラメータ (TABLE III 参照) に対する帯域幅使用量とエントロピーをプロットして得られた曲線を示している。各手法の最も成功した構成に対応する数値結果を TABLE IV に示してる。最も低い帯域使用量は 2 つのマークル木調整手法 (Merkle tree reconciliation method) である。どちらも Scuttlebutt 調整よりはるかに効率的であり、エントロピー指標の悪化やメッセージ配信遅延の犠牲を招くことはない。Figure 4 は様々な手法の帯域幅使用量の時間経過を示している。マークル検索木は、評価したすべての指標においてマークルプレフィクス木と比較してもわずかな優位性を示している。
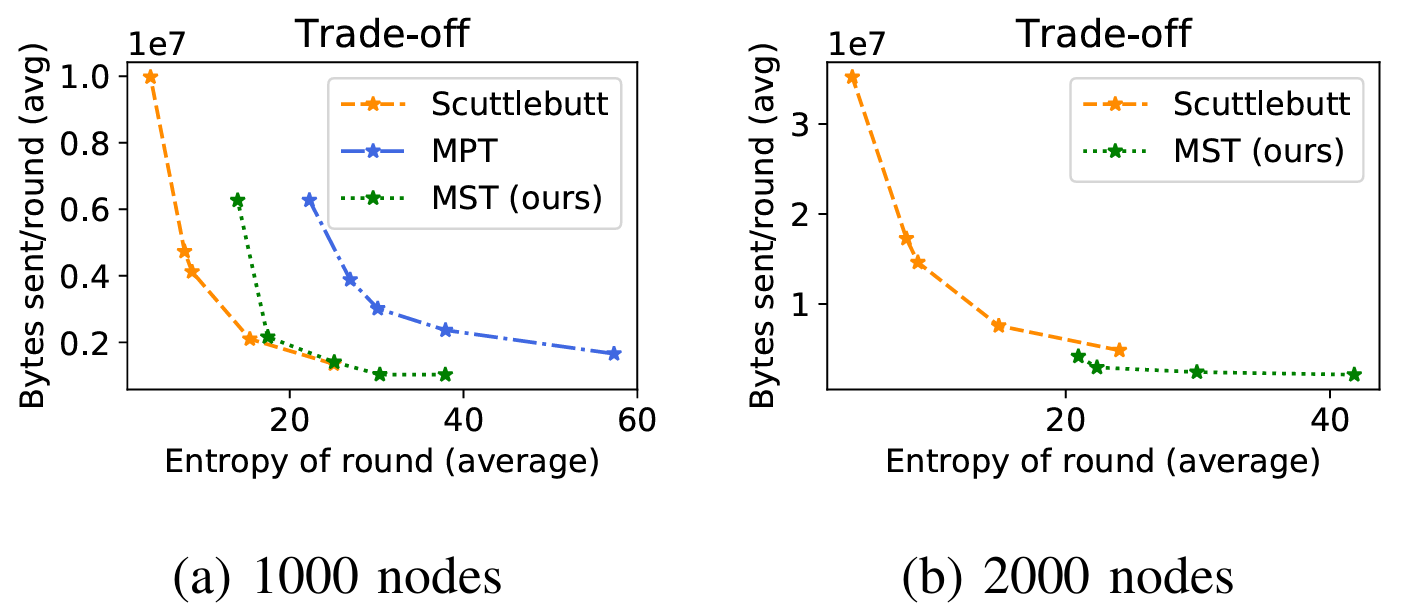
イベント発生率が 10 倍高い 2 番目のシナリオはより曖昧な結果となる。1000 ノードではどちらの手法も同等のパフォーマンスを示す (Figure 3a)。ノード数を 2000 に増やすとマークル検索木のアプローチが Scuttlebutt アプローチよりも優れたスケーラビリティを示すことが分かる (Figure 3b および TABLE V)。このシナリオではマークル検索木のマークルプレフィクス木に対する優位性も明確に示されている。後者は 1000 ノードで両アプローチより悪い結果を示しており、2000 ノードでの実験は終了せず、シミュレーションを完了できなかった。
| 手法 | 帯域幅使用b | エントロピーc | 99% 配信遅延 |
|---|---|---|---|
| Scuttlebutt | 1.3 Mo | 1.61 | 64 ラウンド |
| MPT | 0.51 Mo | 1.44 | 56 ラウンド |
| MST (我々) | 0.44 Mo | 1.06 | 44 ラウンド |
| ゲイン vs. SB | -66% | -34% | -31% |
| ゲイン vs. MPT | -13% | -26% | -21% |
| 1000 ノード | |||
| 手法 | 帯域幅使用 | エントロピー | 99% 配信遅延 |
|---|---|---|---|
| Scuttlebutt | 2.1 Mo | 15.4 | 50 ラウンド |
| MPT | 3.9 Mo | 26.9 | 100 ラウンド |
| MST (我々) | 2.2 Mo | 17.5 | 74 ラウンド |
| 2000 ノード | |||
| Scuttlebutt | 7.6 Mo | 14.9 | 54 ラウンド |
| MPT | -d | - | - |
| MST (我々) | 4.2 Mo | 21.0 | 88 ラウンド |
- b平均して1ラウンドあたり
- c各ラウンドで平均して
- d実験は終了しなかった
2) メッセージ配信遅延: ネットワーク内のイベントのラウンド単位で配信遅延を測定した。99 パーセンタイルの最悪ケースシナリオを検討する。低負荷のケースではマークル検索木が Scuttlebut に対して優位であることを示し (TABLE IV)、高負荷のシナリオでは我々の手法が約 50% の許容可能な性能劣化を提供することを示した (TABLE V)。
3) どのような場合に我々の方が良いか?: Figure 5 に、マークル検索木が Scuttlebutt 手法よりも適している条件を分ける理論的な境界を示した。この境界は TABLE II の理論的結果に基づいて境界での等価性を記述し、アンチエントロピーラウンドにおける差異数 \(d\) をネットワーク内のイベント発生率 \(r\) に置き換えることで使用された: \[ \alpha p + \beta r = r \log_B n \] ここで \(p\) はシミュレーションにおけるプロセス数である。\(\log_B n\) は定数とする (これは \(\log_B N\) と等しく、\(N\) はシミュレーションで生成されるイベントの総数である)。項を並べ換えるとアフィン境界が得られる: \[ r = ap + b \] この境界を 2 つのシミュレーションで較正したところ、どちらの手法も良好なパフォーマンスを示した。1 つは \(p=1000\), \(r=1\) の Figure 3(a) であり、もう 1 つは示されていないが、\(p=500\), \(r=.33\) である。Figure 5 のプロットには完全なシミュレーション集合を実行した実験較正も示されており、各手法が優位性を持つ領域が明確に示されている。
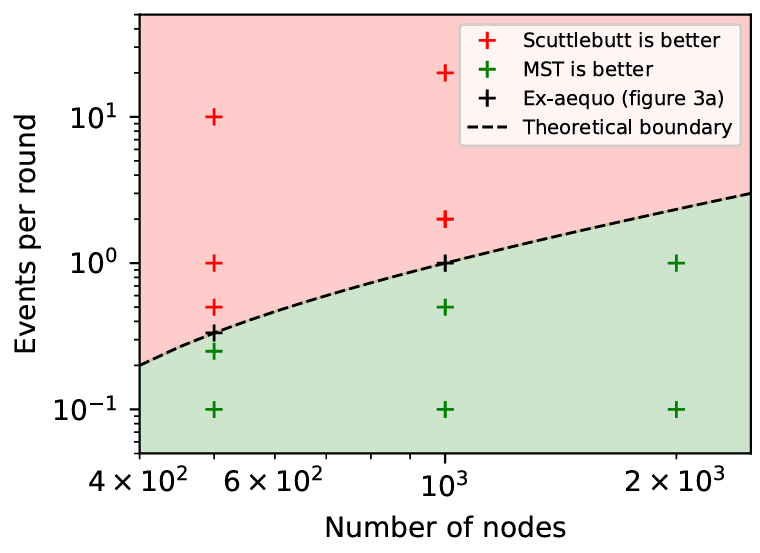
4) 総合評価: 予想通り、マークル検索木はイベント発生率が中程度から低い場合に効率的である。この状況では Scuttlebutt 手法のオーバーヘッドが許容範囲を超えている。
低負荷シナリオでは、マークル検索木は研究した 3 つの指標 (エントロピー、帯域幅使用、99 パーセンタイル配信遅延) において他のすべての手法を上回る性能を発揮した。高負荷シナリオではマークル検索木は Scuttlebutt プロトコルほど低いエントロピーを提供することはできないが、Scuttlebutt の異なる構成で開始されたトレードオフを、より低い帯域幅使用量とエントロピーの向上という方向に拡張することができる。マークル検索木はネットワークに依存するノード数に応じて適切にスケーリングされる。これは、通信コストが参加ノードではなくメッセージの率にのみ依存するためである。
我々はまた、マークル検索木がすべてのシナリオにおいてエントロピーと帯域幅使用量の両方において標準的なプレフィクス木を明確に上回る性能を示すことで、ランダムプレフィクス木がこのアプリケーションに最適ではないという我々の予想を裏付けている。
我々はノードの参加や離脱がない構成のみを研究したが、オープンネットワークではベクタークロックが非アクティブノードの値を蓄積し、アンチエントロピーラウンドごとに無用なメタデータが交換されることになるため、Scuttlebutt 手法のオーバーヘッドがさらに悪化すると推測される。
 VII. 結論と展望
VII. 結論と展望
この論文では、値の集合の効率的な遠隔比較を可能にするマークル木に基づく新しいデータ構造を導入した。このデータ構造を用いることで、非常に大きな状態であっても 2 つの完全な状態間の CRDT マージ演算子を効率的に実装できることを示した。これにより、一般的なデルタベースの手法に必須となる因果ブロードキャストなどのプリミティブを必要とすることなく、オープンネットワーク上で CRDT を複製することが可能となり、参加/離脱を伴うオープンネットワークの世界において独自の優位性を持つ。我々のシミュレーションでは、特に大規模ネットワークにおいて更新率が低い状況において、事前知識なしに変更を検出するのにベクタークロックよりも効率的であることを示した。
マークル検索木の実験的評価は、既知の最も単純な CRDT の 1 つである成長専用集合と同等のイベントストアを構築するという、非常に狭い問題に制限されていた。我々はまた、分散調整プロセスを駆動するために非常に単純なゴシップベースのアルゴリズムにも焦点を当てた。他にも多くの応用や、より複雑なアルゴリズムを想定することができる。このセクションではこれらの展望のいくつかについて説明する。
 A. 適応アルゴリズム
A. 適応アルゴリズム
我々の実験的評価では、ベクタークロックに基づく Scuttlebutt アンチエントロピーとマークル検索木という 2 つの異なる手法を検討した。実験の評価はネットワークが大規模でイベントがしきい値以下の頻度で生成される場合、マークル検索木が Scuttlebutt を明らかに上回る性能を示すことが示された (Figure 5)。観測されたシステムメトリクスに応じて最適なアンチエントロピー手法を自動的に選択する適応アルゴリズムを構築できる。このようなアルゴリズムはワークロード条件の変化に応じてアルゴリズムを動的に切り替えることで、帯域幅使用コストを最小限に抑えながら最高の性能を実現できる。
 B. 永続データ構造としてのマークル DAG
B. 永続データ構造としてのマークル DAG
多くのデータ構造は、標準的なポインタを参照先ブロックのハッシュ値に変更するだけでマークル木またはマークル DAG [18] に符号化できる。これにより、関数型プログラミング言語における永続データ構造 [27] のようにルートハッシュを操作することでデータ構造全体の操作が可能となる。マシンローカルな標準的なポインタとは異なり、マークルハッシュは別のノードに存在するデータへの参照を可能にするため、非常に大規模な分断データ構造の構築が実用的になる。CRDT はデータ構造が決定論的で操作順序に依存しない特定のケースであり、これにより比較と調整の効率的な実装が可能になる。
ルートマークルハッシュを永続データ構造への用意に交換可能なポインタと見なすことで、分散プログラミングへの関数型プログラミング的アプローチが実現され、システム全体の一貫性について考察し実装するための興味深い道筋を開くと我々は信じている。これは、マークルデータ構造をストレージそのものとして使用することを意味し、ノード障害後の調整や修復を達成する方法としてだけではない。
 C. マークル検索木の他のアプリケーション
C. マークル検索木の他のアプリケーション
1) 他の CRDT を最適化するプリミティブとして: 木形状の CRDT は既に提案されており [28]、Treedoc [28] や LSEQ [30] などのシーケンス CRDT で使用されている。これらの手法は、重要な制限事項として既に認識されている平衡調整の問題を回避するために、マークル検索木に類似した構成から恩恵を受ける可能性がある [28]。従来の解決策ではネットワーク全体を同期させ、すべてのノードで同時に木の平衡を調整する提案がなされていた。デフォルトで常に平衡が調整される構成を使用することで、大規模ネットワークまたはオープンネットワークでは非現実的なこの要件を排除できる。
2) 他の CRDT と組み合わせ: 様々な CRDT を値型 \(\mathbb{V}\) として使用することで、マークル探索木のデータ構造を使用して多くの合成 CRDT 型を作成できる。順序付き Key-Value ストアは値型 \(\mathbb{V}\) として last-write-wins レジスタまたは多値レジスタを値型 \(\mathbb{V}\) として使用することで自然に実装できる。削除をサポートする集合や多値マップなど、因果関係を追跡する必要のある CRDT 型の場合、この単純な構成では因果関係の追跡に必要な情報を各項目と共に保存することを意味し、潜在的に大量の冗長なデータを生成する可能性がある。この問題は、因果関係メタデータを個別に格納することで解決できる。
スナップショット分離に類似しているがより弱いトランザクションは、他のアプローチ [31] のように分散ロックを必要とせずにこのようなシステムで容易に実装できる。スナップショット分離の最初の保証である「トランザクションの読み取りがすべてのデータベースの一貫したスナップショット上で実行される」ことは、トランザクション中に他のピアからの更新を統合しないという単純な方法で実現できる。トランザクションが完了すると、生成された更新の集合が伝播され、他のノードで生成された更新も統合される。これらの更新はすべて CRDT 調整ルールを使用して競合を解決する。マークルデータ構造の使用により、データの多くがノードに分散されている場合でも、すべてのデータがコンテンツアドレス指定され、ハッシュによって識別される不変のブロックで構成されるため、このようなスナップショットを簡単に維持できる。このモデルでは、書き込み操作は既存のブロックの読み取りと他のノードによって現在参照されている他のブロックの存在と使用可能性には影響を与えない、新しいブロックの生成のみで構成される。
3) セカンダリインデックスデータ構造として: マークル検索木は RDBMS のインデックスに使用される B-Tree に類似した二次データ構造としても使用できる。つまり、ノード間で共有され DHT に格納される大規模データセットをマークル検索木でインデックス化することで、大規模なピアツーピアネットワークにおいて効率的な検索と SQL のようなプリミティブを実装できる。このような用途を大規模データセットに拡張するには、DHT を使用してマークル検索木のデータブロックをノード間で分散できるかどうかが重要である。多数のノードで同時の更新が発生する場合のこのような手法の実現可能性はまだ評価されておらず、例えば Tamassia と Triandopulos [19] の研究を拡張するなどして今後の研究で探求したいと考えている。
4) ベクタークロック情報の保持: 我々は Scuttlebutt とマークル検索木を 2 つの競合する手法として提示した。しかしこれらは組み合わせることもできる。例えば Scuttlebutt を拡張し、マークル検索木を使用してベクタークロック情報を格納すると、すべてのクロックデータを交換することなく新しいイベントを生成したノードを見つけることが可能となる。
 ACKNOWLEDGEMENTS
ACKNOWLEDGEMENTS
This work has been partially supported by the French ANR projects DESCARTES n. ANR-16-CE40-0023, and PAMELA n. ANR-16-CE23-0016.
 References
References
- N. Bronson, Z. Amsden, G. Cabrera, P. Chakka, P. Dimov, H. Ding, J. Ferris, A. Giardullo, S. Kulkarni, H. Li, M. Marchukov, D. Petrov, L. Puzar, Y. J. Song, and V. Venkataramani, “TAO: Facebook’s Distributed Data Store for the Social Graph,” 2013.
- W. Vogels, “Eventually Consistent,” Queue, vol. 6, Oct. 2008.
- M. Shapiro, N. Preguic ¸a, C. Baquero, and M. Zawirski, “ConflictFree Replicated Data Types,” in Stabilization, Safety, and Security of Distributed Systems, Springer Berlin Heidelberg, 2011.
- P. S. Almeida, A. Shoker, and C. Baquero, “Efficient state-based crdts by delta-mutation,” arXiv:1410.2803 [cs], 2014.
- A. van der Linde, J. Leitão, and N. Preguiça, “\(\delta\)-crdts: Making \(\delta\)-crdts delta-based,” PaPoC ’16, p. 12:1–12:4, ACM, 2016.
- B. Nédelec, P. Molli, and A. Mostéfaoui, “Breaking the Scalability Barrier of Causal Broadcast for Large and Dynamic Systems,” arXiv:1805.05201 [cs], May 2018.
- R. J. T. Goncalves, P. S. Almeida, C. Baquero, and V. Fonte, “DottedDB: Anti-Entropy without Merkle Trees, Deletes without Tombstones,” in SRDS ’17, 2017.
- R. C. Merkle, “A digital signature based on a conventional encryption function,” 1987.
- G. DeCandia, D. Hastorun, M. Jampani, G. Kakulapati, A. Lakshman, A. Pilchin, S. Sivasubramanian, P. Vosshall, and W. Vogels, “Dynamo: Amazon’s Highly Available Key-value Store,” p. 16, 2007.
- R. van Renesse, D. Dumitriu, V. Gough, and C. Thomas, “Efficient Reconciliation and Flow Control for Anti-entropy Protocols,” LADIS ’08, ACM, 2008.
- A. Fox and E. A. Brewer, “Harvest, yield, and scalable tolerant systems,” pp. 174–178, 1999.
- S. Gilbert and N. Lynch, “Brewer’s Conjecture and the Feasibility of Consistent, Available, Partition-tolerant Web Services,” SIGACT News, 2002.
- A. Demers, D. Greene, C. Houser, W. Irish, J. Larson, S. Shenker, H. Sturgis, D. Swinehart, and D. Terry, “Epidemic algorithms for replicated database maintenance,” 1987.
- M. Jelasity, S. Voulgaris, R. Guerraoui, A.-M. Kermarrec, and M. van Steen, “Gossip-based peer sampling,” ACM Trans. Comput. Syst., 2007.
- A. Kermarrec, L. Massoulie, and A. J. Ganesh, “Probabilistic reliable dissemination in large-scale systems,” IEEE Transactions on Parallel and Distributed Systems, vol. 14, pp. 248–258, Mar. 2003.
- P. Euster, R. Guerraoui, A.-M. Kermarrec, and L. Maussoulie, “From epidemics to distributed computing,” IEEE Computer, 2004.
- Y. Zhang, A. Rajimwale, A. C. Arpaci-Dusseau, and R. H. ArpaciDusseau, “End-to-end data integrity for file systems: A zfs case study.,” in FAST, pp. 29–42, 2010.
- J. Benet, “Ipfs-content addressed, versioned, p2p file system,” arXiv preprint arXiv:1407.3561, 2014.
- R. Tamassia and N. Triandopoulos, “Efficient Content Authentication in Peer-to-Peer Networks,” in Applied Cryptography and Network Security, Springer Berlin Heidelberg, 2007.
- S. A. Crosby and D. S. Wallach, “Super-Efficient Aggregating HistoryIndependent Persistent Authenticated Dictionaries,” in ESORICS, 2009.
- R. Bayer and E. M. McCreight, “Organization and maintenance of large ordered indexes,” ACM, 1970.
- B. H. Bloom, “Space/time trade-offs in hash coding with allowable errors,” Commun. ACM, vol. 13, no. 7, pp. 422–426, 1970.
- J. Byers, J. Considine, and M. Mitzenmacher, “Fast approximate reconciliation of set differences,” p. 17, 2002.
- Y. Minsky, A. Trachtenberg, and R. Zippel, “Set reconciliation with nearly optimal communication complexity,” IEEE Transactions on Information Theory, vol. 49, p. 2213–2218, Sep 2003.
- L. Lamport, “Time, Clocks, and the Ordering of Events in a Distributed System,” Commun. ACM, vol. 21, pp. 558–565, July 1978.
- R. Friedman and S. Manor, “Causal Ordering in Deterministic Overlay Networks,” Tech. Rep. CS Technion report CS-2004-04, 2004.
- J. R. Driscoll, N. Sarnak, D. D. Sleator, and R. E. Tarjan, “Making Data Structures Persistent,” STOC ’86, (New York, NY, USA), ACM, 1986.
- M. Shapiro, A comprehensive study of Convergent and Commutative Replicated Data Types, p. 1–5. Springer New York, 2011.
- N. Preguica, J. M. Marques, M. Shapiro, and M. Letia, “A Commutative Replicated Data Type for Cooperative Editing,” in 29th IEEE International Conference on Distributed Computing Systems, 2009.
- B. Nédelec, P. Molli, A. Mostefaoui, and E. Desmontils, “LSEQ: An Adaptive Structure for Sequences in Distributed Collaborative Editing,” DocEng ’13, ACM, 2013.
- T. Schütt, F. Schintke, and A. Reinefeld, “Scalaris: reliable transactional p2p key/value store,” in ERLANG ’08, p. 41, ACM Press, 2008.
翻訳抄
キーの順序を維持しながら決定論的に平衡 (バランス) を維持するマークル検索木 (MST) を提案する 2019 年の論文。従来の CRDT 実装はベクタークロックのような因果ブロードキャストに依存しているため大規模ネットワークやオープンネットワークで効率的に実装するのは難しいが、MST によりそのようなネットワーク上で状態ベース CRDT を効率的に実装できる。
- Alex Auvolat, François Taïani. Merkle Search Trees: Efficient State-Based CRDTs in Open Networks. SRDS 2019 - 38th IEEE International Symposium on Reliable Distributed Systems, Oct 2019, Lyon, France. pp.1-10, ff10.1109/SRDS.2019.00032ff. ffhal-02303490f
